Histograma? Qué es y como elaborarlo

Los histogramas son una forma de resumir una variable numérica continua. Se usan para  mostrar la distribución general. Sin embargo, pueden ser sensibles a las opciones de parámetros! Vamos a llevarlo paso a paso a través de las consideraciones con muchas visualizaciones de datos. Si hay algo que no entienda después de leer el ensayo, puede contactarnos; Nuestra información de contacto está al final y en el perfil del blog. ¡Comentarios y sugerencias son bienvenidos!

Al recolectar los datos,  de una sola variable, lo primero es pensar como lo vamos  a ordenar y a clasificar,  nos centramos, en la forma de visualizar  una distribución, ella  depende de si la variable de interés es categórica o numérica, es decir, si la variable es cualitativa,  cuantitativa  discreta o cuantitativa  continua.

Variables categóricas o cualitativas y sus distribuciones.

Las variables categóricas toman solo unos pocos valores específicos. Por ejemplo, el género es una variable categórica común, quizás con las categorías "masculino", "femenino" y "no conforme con el género".

Para visualizar la distribución de una variable categórica, usamos lo que se llama un gráfico de barras, estos muestran cuántos elementos se cuentan en cada conjunto de categorías. Por ejemplo, el siguiente gráfico de barras se realizó con la finalidad de ver gráficamente cuantos estudiantes o alumnos realizan  cursos en la academia fz .

 Es una variable cualitativa nominal, donde se cuenta  cuántas personas hay en cada curso de programación.

Debido a su naturaleza discreta, no hay mucho que decidir al dibujar un gráfico de barras. Un analista puede elegir el orden de las categorías, el color de las barras y la relación de aspecto, para visualizar dicho información.

Variables numéricas (Cuantitativas Discreta o Continua) y sus distribuciones.

Las variables numéricas se miden como números. La altura es numérica, a menudo se mide en centímetros o pulgadas. La edad es numérica, medida en años o días. Las variables numéricas pueden ser discretas o continuas . Las variables discretas solo toman valores enteros (1, 2, 3, etc.). Las variables continuas toman cualquier valor a lo largo de la línea numérica o el conjunto de números reales (1.7, 14.06, etc.).

Cuando una variable es numérica, su distribución se puede representar de varias maneras ; Probablemente el método más común es el histograma.

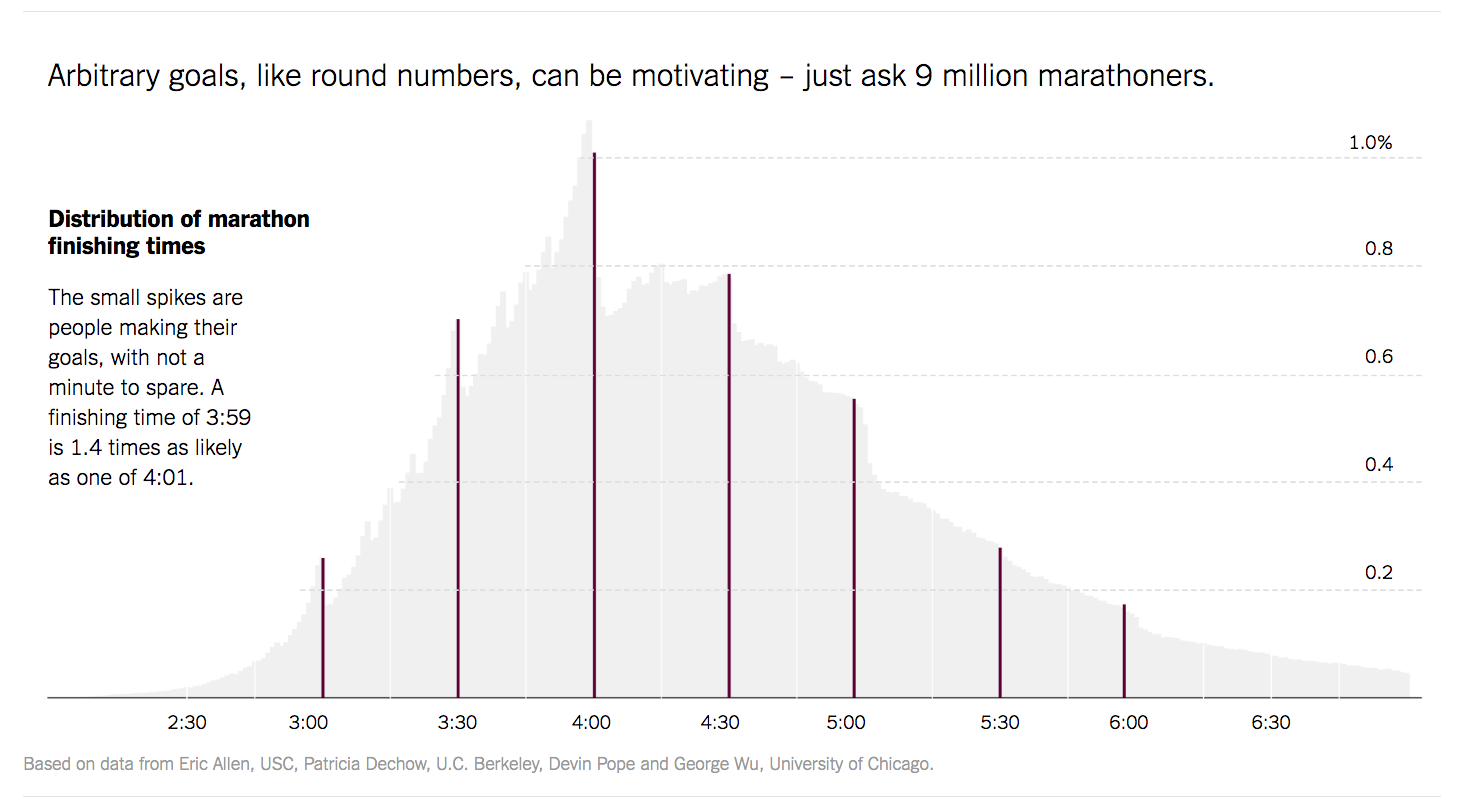
Justin Wolfers de The Upshot produjo el histograma de la siguiente figura para visualizar los tiempos finales de 10 millones de corredores de una maratón.

A primera vista, la creación de un histograma parece bastante simple: dividimos los datos en un conjunto de contenedores, cajas o grupos, discretos, luego contamos cuántos valores caen en cada uno de los grupos. Pero, al observar más detenidamente, vemos que en realidad hay muchas opciones que se deben tomar para crear un histograma que represente fielmente la forma de la distribución.

Cómo construir un histograma

Reúne tus datos

Un histograma se basa en una recopilación de datos sobre una variable numérica. Nuestro primer paso es reunir algunos valores para esa variable.  Podemos visualizar el conjunto de datos como un conjunto de elementos, con cada elemento identificado por su valor, que en teoría nos permite "ver" todos los elementos, pero hace que sea difícil obtener un comportamiento de la variable. ¿Cuáles son algunos valores comunes? ¿Hay mucha variación?

Ordenar en una lista 

Un primer paso útil para describir la distribución de la variable es ordenar los elementos en una lista. Ahora podemos ver el valor máximo y el valor mínimo. Más allá de eso, es difícil decir mucho sobre el centro, la forma y la distribución de la distribución. Parte del problema es que la lista está completamente llena; el espacio entre dos elementos es el mismo, sin importar cuán diferentes sean sus valores. Necesitamos una forma de ver cómo los elementos se relacionan entre sí. ¿Están agrupados alrededor de unos pocos valores específicos? ¿Hay un objeto solitario con un valor muy alejado de todos los demás?

Construye la Distribución de Frecuencias

Obtén el Rango, ======>>>>>      Rango = Valor Mayor - Valor Menor, esto es para determinar el intervalo total, donde estarán comprendidos todos los valores de la serie de datos a estudiar.

Luego tienes que decidir el número de intervalos de clases a realizar, no hay reglas para esta decisión, todos los métodos existentes son empíricos, según las bibliografias de Estadísticas mas famosas en el tema. Se recomienda hacer distribuciones de frecuencias que tengan mínimo cuatro (4) intervalos de clases, máximo siete (7), ya que su visualización es aceptada en la mayoría de los casos. Los intervalos de clases deben ser, siempre que sea posible, iguales, a fin de de que la comparabilidad entre las frecuencias de las diversas clases se torne fácil. El intervalo de clase no debe ser tan grande que oculte las características más importantes de la variable a estudiar.

luego de obtener el Rango y el Número de Intervalos. se realiza el cálculo del Tamaño de cada Intervalo o intervalo de Clases.

Rango = (VM - Vm) ;       NI =Número de Intervalos

Tamaño del Intervalo =Rango/Número de Intervalos

Un procedimiento alternativo para determinar el intervalo de clase o tamaño del intervalo, ha sido sugerido por H.A. Sturges, aplicando la siguiente fórmula:

Tamaño del Intervalo = Rango/( 1+3,322*log(N))

Esta fórmula da valores fraccionarios no adecuados para su uso en la práctica; sin embargo, podemos aplicar las reglas de redondeo y convertirlos en enteros o eliminar algunos decimales en cuanto sea posible. 

Es importante indicar con precisión los limites de las clases y evitar clasificaciones como estas:

0--------10
10------20
20------30

como se observa los valores 10 y 20 pertenecen a dos clases, los cuales cuando estemos registrando las frecuencias se realizarían dobles. Tampoco se debe escribir: 

más de  0   menos de 10
más de 10  menos de 20

ya que el valor de 10 no pertenece a ninguna de las  clases citadas.

Una forma de presentación de clases que  se sugiere es:
 0-----9,9
10---19,9 
20---29,9
30---40
la cual no presenta los vicios señalados anteriormente

otra clasificación correcta es para variables discretas
10------19
20------29
30------39
40------49
50------59

Una vez , construidos los intervalos de clases, registramos la frecuencia que tiene los datos de la variable a estudiar, en cada uno de los intervalos de clases, ya una vez  obtenida la distribución de frecuencias, se dibuja los ejes de coordenadas sobre el plano

En el eje de las abscisas (x), se coloca los intervalos de clases y sobre el eje de las ordenadas la magnitud de cada frecuencia,  luego se levantan rectángulos o barras en cada clase formada.

En el caso del maratón, por ejemplo,  el tiempo mínimo fue 2 horas, y el tiempo máximo de los maratonista fue de 5 horas.

Hallamos el rango. Rango = 5-2 = 3

Luego decidimos que el número de intervalos es 6.

Hallamos el Tamaño de cada intervalos es Ic = 3/6 = 1/2 =0.5

Construimos la Distribución de Frecuencias

             Distribución de frecuencia
Se escribe la variable          Frecuencia
                       ↓                           ↓
Tiempo en horas y minutos N° de personas
2,00 ------------------2,5                  99
2,501-----------------3,0                201
3,001-----------------3,5                450
3,501-----------------4,0                350
4,001-----------------4,5                188
4,501-----------------5,0                112
Total                                       1400

En excel sería  así:

La Gráfica o Histograma, del lado del eje de las ordenadas, se levanta la columna del N° de personas, y del lado del eje de las abscisas, se construyen los intervalos de clases, en este caso: las horas del tiempo de la maratón, las cuales fueron agrupadas por cada media hora.

Preguntas : Porqué se seleccionó 6 intervalos de clases?

Cuál es la distribución de los datos? 

Los histogramas proporcionan una forma de visualizar datos agregándolos en barras, y se pueden utilizar con datos de cualquier tamaño.

La división de elementos en las barras: la esencia de un histograma

Reunir los datos en barras nos ayuda a responder la pregunta "¿Cómo es la distribución de estos datos?" Imagine, que ud. intenta describir algunos conjuntos de datos, que le están comunicando por teléfono, en lugar de leer mecánicamente toda la lista de valores, sería más útil proporcionar un resumen, como para poder decir, si la distribución de la variable es simétrica, dónde está centrada y si tiene valores extremos, etc. Un histograma es otro tipo de resumen, en el que se comunican las propiedades generales en términos de porciones (es decir, barras) de los datos

Tal vez porque los histogramas son visualmente similares a los gráficos de barras, es fácil pensar que también son objetivos similares. Pero, a diferencia de los gráficos de barras, los histogramas se rigen por que se visualizan las variables cuantitativas continuas, donde un intervalo tiene inmediatamente la secuencia del otro en términos de números reales.Además, podemos señalar que antes de describir un conjunto de datos a alguien, en función de lo que ve en su histograma, debe saber si los diferentes valores de los parámetros podrían haberlo llevado a diferentes descripciones.

Lo importante es que un histograma,  es un resumen representativo de un conjunto de datos subyacente.

En la figura del histograma anterior que se puede visualizar? Cual es el comportamiento de la variable? Que podemos decir de los datos?  Se observa la data o distribución simétrica? Que conclusiones podemos sacar de la gráfica? 

Con este pequeño ejemplo, espero haber ayudado un poco a resolver la construcción del Histograma, si tienes alguna duda, deja tu comentario o escribe al correo zavafree@gmail.com que con gusto trataré de aclarar las dudas.

El análisis de datos Estadístico y su impacto en el Deporte

Los datos se están convirtiendo en el nuevo enfoque de muchos sectores, pero  el foco en en mundo de los deportes lo tiene  la Estadística, donde se ha hecho de gran influencia y ha empezado a generar por medio de la tecnología un gran avance en el conocimiento de dichas actividades y lo que viene parece que es,  muy prometedor!.. en todos los deportes es imprescindible llevar estadísticas, aquí mostraremos avances en dos áreas que son el beisbol y el futbol, pero sin perder la idea y de vista, de lo maravilloso que la estadística y la tecnología están aportado a nuestra vida deportiva.

El béisbol ya vivió este cambio cuando Billy Beane, entrenador de los Oakland Athletics, revolucionó este deporte en los años 90 al ser el primero en usar la inteligencia de datos.

En esa época todo se basaba en los grandes presupuestos y en tener grandes estrellas en el equipo. Los fichajes se conseguían en base a los Scouts ( busca talentos ), que visitaban los distintos estados y stadiums buscando nuevos peloteros, pero se basaban en su intuición, experiencia y muy poca información estadística de los jugadores.

Los Oakland Athletics no tenían medios económicos y Billy empezó a colaborar con un joven estudiante de economía llamado Paul DePodesta en un sistema estadístico que predijese los jugadores más “rentables” (que aportasen más carreras por menos dinero) en base a sus estadísticas de juego.

 “Las personas que dirigen los equipos piensan en comprar jugadores. No deberían pensar en comprar jugadores, sino victorias. Y para eso, necesitan comprar carreras"

Sabermetría es ayudar a tomar mejores decisiones dentro del béisbol.

La sabermetría no es más que el análisis del béisbol a través de evidencia objetiva, específicamente a través de estadísticas, cuyo objetivo es medir las actividades que se suscitan dentro de un campo de juego de manera eficaz. El término es derivado del acrónimo SABR, el cual según sus siglas en inglés hace referencia a la Sociedad para la Investigación del Béisbol Americano (Society for American Baseball Research), la cual fue fundada en 1971 por Bob Davis. Pero el término sabermetrics no fue acuñado sino hasta 1980 por Bill James, quien hizo referencia al mismo a través de sus escritos sobre béisbol conocidos como Baseball Abstracts, sobre los cuales hablaremos más adelante.

Para ser más especifico, la Sabermetría se concentra en evaluar formas de medición para un propósito en concreto, el cual está enfocado en conocer cómo afectan las estadísticas individuales y colectivas, al record de ganados y perdidos de un equipo de béisbol. La lógica detrás de ésto es que para que un equipo sea exitoso debe ganar más juegos que sus oponentes, lo que se logra mediante la anotación copiosa de carreras o por medio de la prevención de éstas.

La siguiente gráfica fue realizada con una técnica de análisis de datos denominada "cluster", ahí se compara el valor relativo de los jugadores de béisbol altamente remunerados que utilizan el salario y el WAR de un jugador, una estadística de béisbol que resume las contribuciones totales de un jugador a su equipo.WAR significa "Wins Above Replacement". Cuanto mayor sea WAR, mejor será el jugador.

La Estadística esta dando muchos logros en esta área, apoyada por la tecnología y es de gran apoyo para la toma de decisiones

En el fútbol actual,  el Análisis de Datos Estadístico está impactando este deporte 

Como observaremos a continuación, los datos estadísticos son el nuevo oro, y los diferentes clubs y organizaciones de fútbol están recopilando todos los datos posibles porque saben que les proporcionarán una ventaja competitiva, en las siguientes aristas:




Entrenador: La mejora de la estrategia
Jugadores: La mejora de la técnica
Fanáticos: La mejora de la experiencia
Equipo Médico: La mejora de la predicción de lesiones
Apuestas: La predicción de eventos de partido y resultados

1. Entrenador: La mejora de la estrategia

Un punto clave donde las herramientas de predicción basada en datos estadísticos, pueden ayudar es en el análisis de la estrategia planteada para el partido y la predicción del resultado. En este ámbito se están haciendo muchos avances, y un ejemplo de ello es el proyecto de Disney Research (sí, los de Mickey Mouse) que utiliza Deep Learning y el método “Data-Driven Ghosting” para predecir la probabilidad de gol en una jugada defensiva de tu equipo versus como la hubiese defendido un equipo típico o medio de tu liga. De este modo, puedes analizar si los movimientos de tu defensa son mejores o peores que la media en un tipo de jugada concreta y mejorarlos

2. Jugadores: La mejora de la técnica

Hace ya algunos años que los dispositivos de recopilación de datos de juego están proliferando en el mundo del fútbol. Conocidos como “wearables“, son dispositivos electrónicos inteligentes incorporados a la vestimenta y que nos permiten recoger datos médicos (pulsaciones, respiración, temperatura, etc.) y físicos (posición, velocidad, aceleración, etc.) del jugador durante el entrenamiento y los partidos. Un ejemplo es la tecnología EPTS de la FIFA que, gracias a dispositivos insertados en los tops interiores de los jugadores, pueden recoger todos los datos de juego. Otra iniciativa interesante es la de la empresa PlayerMaker, que opta por wearables en las botas para poder recoger además datos del golpeo, % de uso de cada pierna o control del balón.

También Microsoft esta invirtiendo en este tipo de soluciones con su proyecto Sports Performance Platform con el que han recogido datos equipos como la Real Sociedad y presentado los resultados en esta nueva plataforma de análisis.

3. Fanáticos: La mejora de la experiencia

Los clubs saben que los fanáticos son la base de su negocio. Por ello, están invirtiendo mucho dinero en tres áreas relacionadas con ellos:

El análisis de lo que hacen sus fanáticos en los estadios para mejorar la experiencia de ir a ver un partido

Un ejemplo de ello nos lo puede proporcionar SAP con su solución Venue Analytics. En ella se puede controlar la asistencia, grado de satisfacción, ocupación de parkings cercanos al estadio, etc. La mejora de la experiencia de retransmisión para los fanáticos que lo siguen por la televisión. as empresas de telecomunicaciones siempre han sido conscientes de lo importante que suponen las retransmisiones de eventos deportivos, pero ahora ya no es suficiente con ofrecer el evento: el público quiere experiencias adicionales y la mejor calidad de imagen. En este sentido, están intentando optimizar esta experiencia proporcionando estadísticas y datos adicionales al telespectador gracias al análisis del vídeo en tiempo real. El siguiente vídeo muestra un ejemplo en el que la empresa SentioScope usa este tipo de tecnologías para predecir el jugador y hacerle seguimiento en tiempo real en la imagen mostrada y así poder obtener estadísticas de distancia recorrida:

Realización de encuestas para obtener datos de los fanáticos para realizar campañas de marketing más personalizadas y efectivas.Hace tiempo que los clubs saben que su relación con los fanáticos no se limitan a los días de partido. Deben crear conexiones con ellos cada día, por lo tanto se trata de conocer las preferencias de ellos.Un ejemplo es la colaboración de IBM (con su solución Watson), la cadena FOX y la FIFA para el último Mundial en el que crearon la aplicación FIFA World Cup Highlight Machine . Con ella el seguidor puede escoger su selección o jugador, el tipo de jugada que le gusta y el sistema le proporciona en segundos una selección de las jugadas elegidas para que pueda crear su propio vídeo de mejores momentos y compartirlo en redes sociales.

El fanático debe registrarse y dar sus datos, te deja la información de su jugador favorito y de las jugadas que más le han gustado y lo comparte en sus redes sociales. ¿Qué más se puede pedir?

4. Equipo Médico: La mejora de la predicción de lesiones

Volviendo al inicio del post, en 2018 Billy Beane dijo en una conferencia en el OpenText Enterprise World que “El reto hoy es evitar lesiones con datos”.Es por ello que varias empresas se han puesto manos a la obra para intentar diseñar modelos capaces de predecir la probabilidad de lesión y que tipo de lesión de los jugadores.Un reciente estudio sobre La Liga indica que existe una tasa de ausencias por lesión del 16,23% y se calcula que, traducido a dinero, supone unos 188.058.072 €. Con estas cifras, es obvio que cualquier ayuda para su prevención es bien recibida por los clubs.

Gráfica que muestra las lesiones anticipadas por el algoritmo y las que no

Las lesiones pueden ser fortuitas o impredecibles (una jugada desafortunada en un partido), pero según Tim Gabbet (afamado consultor de rendimiento deportivo): “Toda enfermedad relacionada con la carga de trabajo puede considerarse como predecible”. Es por ello que los modelos de predicción se están basando en anticipar este tipo de lesiones provocadas por la carga de trabajo de entrenamientos y partidos oficiales. Un ejemplo de todo ello es  que mediante una cámara térmica puede detectar lesiones en los futbolistas. En este caso usan tecnologías de Deep Learning para reconocer las partes del cuerpo de la imagen y junto con el color de la lectura térmica poder detectar lesiones.

Nuevo algoritmo ThermoHuman

5. Apuestas: La predicción de eventos de partido y resultados

Es sabido por todos que las apuestas deportivas han entrado con fuerza en el mundo del fútbol. Y viendo el potencial que tienen , no es raro ver que  las casas de apuestas que usa inteligencia de datos para sus cuotas, pagos y pronósticos. Si unimos todos los puntos anteriores y tuviésemos acceso a toda esa información (datos físicos de los jugadores, análisis de estrategias, datos online de asistencia al estadio, predicción de lesiones, etc…) y lo juntásemos con el histórico de resultados seguro que encontraríamos un algoritmo bastante ajustado para predecir el resultado de un partido. Aunque ya se sabe, “fútbol es fútbol” y algunos dicen que es imposible de predecir.

IMÁGENES DE DEPORTES Y SU RELACIÓN CON LA ESTADÍSTICA Y LA TECNOLOGÍA

Software de Data Science utilizado en revistas: paquetes de estadísticas en declive (incluida R), AI / ML Software Growing

En mi interminable búsqueda para rastrear artículos de estadística me encontré con el siguiente: la popularidad del software Data Science . El rápido crecimiento de R no podría durar para siempre y, como se verá más adelante, su uso disminuyó en el último año.

Articulos escolares

Los artículos académicos proporcionan una fuente rica de información sobre herramientas de ciencia de datos. Debido a que la publicación requiere una gran cantidad de esfuerzo, el análisis del tipo de herramientas de ciencia de datos que se usa en los artículos académicos brinda una mejor imagen de su popularidad que una simple encuesta sobre el uso de herramientas. Cuanto más popular es un paquete de software, más probable es que aparezca en publicaciones académicas como una herramienta de análisis, o incluso como un objeto de estudio.

Dado que los artículos académicos tienden a utilizar métodos de vanguardia, el software que se utiliza en ellos puede ser un indicador importante de hacia dónde se dirige el mercado general del software de ciencia de datos. Google Scholar ofrece una manera de medir dicha actividad. Sin embargo, ninguna búsqueda de esta magnitud es perfecta; Cada uno incluirá algunos artículos irrelevantes y rechazará algunos relevantes. Los detalles de los términos de búsqueda que utilicé son lo suficientemente complejos como para pasar a un artículo complementario,  Cómo buscar artículos de Data Science . Dado que Google mejora regularmente su algoritmo de búsqueda, cada año recopilo datos nuevamente durante los años anteriores (con una excepción que se detalla a continuación).

La Figura 2a muestra la cantidad de artículos encontrados para los paquetes de software e idiomas más populares (aquellos con al menos 1,700 artículos) en el año completo más reciente, 2018. Para permitir un tiempo suficiente para la publicación, inserción en bases de datos en línea e indización, Datos recogidos el 28/03/2019.

Figura 2a. La cantidad de artículos académicos encontrados en Google Scholar, para software de ciencia de datos. Solo se muestran aquellos con más de 1,700 citas.

SPSS es, con mucho, el paquete más dominante, como lo ha sido durante más de 20 años. Esto puede deberse a su equilibrio entre potencia y facilidad de uso. R está en segundo lugar con alrededor de la mitad de artículos. Ofrece potencia extrema, aunque con menos facilidad de uso . SAS ocupa el tercer lugar, con una ligera ventaja sobre Stata, MATLAB y GraphPad Prism, que están casi empatados.

Tenga en cuenta que los lenguajes de propósito general: C, C ++, C #, FORTRAN, Java, MATLAB y Python se incluyen solo cuando se encuentran en combinación con los términos de ciencia de datos, por lo tanto, considere esos recuentos como más aproximados que el resto.

El siguiente grupo de paquetes va de Python a C, y el uso disminuye lentamente. El siguiente conjunto comienza en Caffe, bajando casi el 50% y continuando a IBM Watson con un lento declive.

Los dos últimos paquetes en la Fig. 2a son Weka y Theano, que son una gota de IBM Watson, aunque cada vez es más difícil ver que las líneas se encogen.

Para continuar en esta escala, todos los paquetes restantes aparecerían demasiado cerca del eje y para leer, por lo que la Figura 2b muestra el software restante en una escala mucho más pequeña, y el eje y va a solo 1,700 en lugar de los 80,000 utilizados en Figura 2a.

Figura 2b. Númerode artículos académicos que usan cada software de ciencia de datos encontrado usando Google Scholar. Solo se muestran aquellos con menos de 1,700 citas.

Elegí comenzar la Figura 2b con un software que tiene menos de 1,700 artículos porque nos permite ver RapidMiner y KNIME en la misma escala. Ambas son herramientas impulsadas por el flujo de trabajo con capacidades muy similares. Esta gráfica muestra RapidMiner con un 49% más de uso que KNIME. RapidMiner utiliza más marketing, mientras que KNIME depende más de recomendaciones de boca en boca y de un modelo de código más abierto. Las firmas consultoras de TI Gartner y Forrester las calificancomo herramientas capaces de defenderse de los titanes comerciales, SPSS y SAS de IBM. Dado que SPSS tiene aproximadamente 50 veces el uso en el mundo académico, eso parece bastante difícil. Sin embargo, como veremos pronto, el uso de estos paquetes más nuevos está creciendo, mientras que el uso de los más antiguos se está reduciendo bastante rápidamente.

La Figura 2b también nos permite ver SPSS Modeler, SAS Enterprise Miner y Alteryx de IBM en la misma gráfica. Estos tres también son herramientas impulsadas por el flujo de trabajo que son bastante caras. Ninguno lo está haciendo tan bien aquí como RapidMiner o KNIME, herramientas mucho menos costosas, o gratuitas, dependiendo de cómo las use (el escritorio de KNIME es gratuito, pero servidorno es; RapidMiner es gratuito para analizar menos de 10,000 casos).

Otra comparación interesante enLa figura 2b es JASP y jamovi . Ambas son herramientas de código abierto que se centran en estadísticas en lugar de aprendizaje automático o inteligencia artificial. Ambos utilizan interfaces gráficas de usuario (GUI) en un estilo que es similar a SPSS. Ambos también usan R detrás de escena para hacer sus cálculos. JASP enfatiza el análisis bayesiano y oculta su código R; jamovi tiene una orientación más frecuente, le permite ver su código R y le permite ejecutar su propio código R directamente desde él. JASP actualmente tiene nueve veces más citas aquí, aunque el uso de jamovis está creciendo mucho más rápidamente.

Incluso más reciente en la GUI para la escena R es BlueSky Statistics , que no aparece en la trama, ya que hasta el momento no tiene artículos académicos. Fue creado por una nueva empresa y solo adoptó un modelo de código abierto hace unos meses.

Si bien las Figuras 2a y 2b son útiles para estudiar la cuota de mercado tal como está ahora, no muestran cómo están cambiando las cosas. Sería ideal contar con gráficos de tendencias de crecimiento a largo plazo para cada uno de los paquetes de análisis, pero la recopilación de esa cantidad de datos anualmente requiere mucho tiempo. En su lugar, lo que he hecho es recopilar datos solo de los últimos dos años completos, 2017 y 2018. Esto proporciona los datos necesarios para estudiar los cambios interanuales.

La Figura 2c muestra el porcentaje de cambio a lo largo de esos años, con los crecientes paquetes "calientes" mostrados en rojo (lado derecho); la disminución o el "enfriamiento" se muestran en azul (lado izquierdo). Dado que la cantidad de artículos tiende a ser de miles o decenas de miles, eliminé cualquier software que tuviera menos de 1,000 artículos en 2015. Un paquete que crece de 1 artículo a 5 puede mostrar un crecimiento del 500%, pero todavía es de poco interés. .

Figura 2c. Cambio en la tasa de citas de Google Scholar en los últimos dos años completos, 2017 y 2018.

Los cambios recientes en el software de ciencia de datos pueden resumirse sucintamente: AI / ML up; estadísticas abajo El software que está creciendo no contiene ninguno de los paquetes que están asociados más con el análisis estadístico. El software en declive está dominado por los paquetes clásicos de estadísticas: SPSS Statistics, SAS, GraphPad Prism, Stata, Statgraphics, R, Statistica, Systat y Minitab. JMP es el único paquete de estadísticas tradicional cuyo uso académico está creciendo. Del software de aprendizaje automático que está disminuyendo en el uso, hay equivalentes aproximados que están creciendo (por ejemplo, Mahout down, Spark up).

De cursootro resumen es: barato (o gratis) arriba; caro hacia abajo. De los paquetes en crecimiento, 13 de los 17 están disponibles en código abierto. De los que están en declive, solo 5 de los 13 son de código abierto.

El software de estadísticas ha existido durante mucho más tiempo que el software AI / ML, se inició en los días anteriores al código abierto. Los proveedores de estadísticas han estado agregando métodos AI / ML a su software, lo que los convierte en las soluciones más completas. A los proveedores o proyectos de AI / ML les está perdiendo la oportunidad de agregar capacidades de estadísticas más completas. Algunos, como RapidMiner y KNIME, se están expandiendo en esta dirección, pero muy lentamente.

En la parte superior de la Figura 2c, vemos que los paquetes de aprendizaje profundo Keras y TensorFlow son los de mayor crecimiento con casi un 150%. PyTorch no se muestra aquí porque no tuvo suficiente uso en el año anterior. Sin embargo, su tasa de citas pasó de 616 a 4,670, ¡una tasa de crecimiento sustancial del 658%! Hay otros paquetes que no se muestran aquí, incluyendo JASP con un crecimiento del 223% y jamovi con un crecimiento del 720%. A pesar de un crecimiento tan alto, este último solo tiene 108 citas en 2018. El rápido crecimiento de JASP y jamovi da credibilidad a la perspectiva de que el patrón general de cambio que se muestra en la Figura 2c puede ser más un resultado del software libre en comparación con el costoso. Ninguno de ellos ofrece ninguna característica de AI / ML.

Scikit Learn, la biblioteca de aprendizaje automático de Python, creció rápidamente con un aumento del 60%.

Me sorprendió ver que IBM Watson creció un 34% de forma saludable, ya que muchas de las noticias no han sido buenas . ¡Aunque es increíble en Jeopardy !

En el concurso RapidMiner vs. KNIME, vimos anteriormente que RapidMiner estaba por delante. A partir de este gráfico, hemos dicho que KNIME está creciendo ligeramente (5.7%), mientras que RapidMiner está disminuyendo ligeramente (1.8%).

Los mayores perdedores en la Figura 2c son SPSS, un 39% menos, y SAS, Prism y Mahout, todos un 24% menos. Incluso R ha bajado un 13%. Recuerde que la Figura 2a muestra que a pesar de los últimos años de declive, SPSS sigue siendo extremadamente dominante para el uso académico, y R y SAS siguen siendo los paquetes más utilizados # 2 y # 3 en esta área.

Estoy particularmente interesado en las tendencias a largo plazo de los paquetes de estadísticas clásicas. Así que en la Figura 2d he trazado los mismos datos de uso académico para 1995 hasta 2016.

Figura 2d. La cantidad de citas de Google Scholar para cada paquete de estadísticas clásicas por año desde 1995 hasta 2016.

SPSS tiene una clara ventaja en general, pero ahora puede ver que su dominio alcanzó su punto máximo en 2009 y su uso está en un fuerte descenso. SAS nunca se acercó al nivel de dominio de SPSS, y su uso alcanzó su punto máximo alrededor de 2010.GraphPADPrism siguió un patrón similar, aunque llegó un poco más tarde, alrededor de 2013.

En la Figura 2d, el dominio extremo de SPSS hace que sea difícil ver las tendencias a largo plazo en el otro software. Para solucionar este problema, he eliminado SPSS y todos los datos de SAS excepto para 2014 y 1015. El resultado se muestra en la Figura 2e.

Figura 2e. La cantidad de citas de Google Scholar para cada paquete de estadísticas clásico desde 1995 hasta 2016, esta vez con SPSS eliminado y SAS incluido solo en 2014 y 2015. La eliminación de SPSS y SASexpandido La escala hace que sea más fácil ver el rápido crecimiento de los paquetes menos populares.

La Figura 2e hace que sea fácil ver que la mayoría de los paquetes restantes crecieron constantemente a lo largo del período de tiempo mostrado. R y Stata crecieron especialmente rápido, al igual que Prism hasta 2012. Tenga en cuenta que la disminución en el número de artículos que usaron SPSS, SAS o Prism no se ve compensada por el aumento en el otro software que se muestra en este gráfico en particular. Incluso sumar todo el otro software que se muestra en las Figuras 2a y 2b no tiene en cuenta la disminución general. Sin embargo, estoy viendo solo 58 de más de 100 herramientas de ciencia de datos.

Mientras que las Figuras 2d y 2e muestran la tendencia histórica que terminó en 2016, la Figura 2f muestra un nuevo conjunto de datos recopilados en Marzo,2019. Dado que el algoritmo de Google cambia, lo que evita que los nuevos datos coincidan exactamente con los antiguos, estos nuevos datos comienzan en 2015, por lo que los dos conjuntos se superponen. SPSS no se muestra en este gráfico porque su predominio comprimiría el eje y, haciendo que las tendencias en los demás sean más difíciles de ver. Sin embargo, tenga en cuenta que a pesar de la caída del 39% de SPSS de 2017 a 2018, ¡su uso sigue siendo un 66% más alto que los R en 2018!Aparentemente La gente está dispuesta a pagar por la facilidad de uso.

Figura 2f. El número de citas de Google Académico para cada paquete de estadísticas clásico por año desde 2015 hasta 2018.

En la Figura 2f podemos ver que las tendencias a la baja de SAS, Prism y Statistica continúan. También vemos que el largo y rápido crecimiento de R y Stata ha llegado a su fin. El crecimiento tan rápido no puede durar para siempre. Será interesante ver el próximo año para ver si esto es simplemente un aplanamiento del uso o el comienzo de una tendencia a la baja. Como señalé en mi libro, R para usuarios de Stata , hay muchos puntos en común entre R y Stata. Como resultado de esto, y el hecho de que R es de código abierto, esperoUso R para estabilizar a este nivel mientras utilizar De Stata sigue disminuyendo lentamente.

El rápido declive a largo plazo de SPSS tiene que nivelarse en algún momento. Han sido destrozados por muchos competidores. Sin embargo, hasta hace poco, estos competidores han sido gratuitos y basados ​​en código, como R, o basados ​​en menús y propietarios, como Prism. Con la reciente llegada de JASP, jamovi y BlueSky Statistics , SPSS ahora enfrenta un software gratuito y basado en menús. Los proyectos anteriores para agregar menús a R, como R Commander y Deducer , también eran gratuitos y de código abierto, pero requerían instalar R por separado y luego usar el código R para activar los menús.

Estos resultados se aplican a artículos académicos en general. Es muy probable que los resultados en campos específicos o revistas sean diferentes.

Para ver muchas otras formas de estimar la participación de mercado de este tipo de software, vea mi artículo en curso,  La popularidad del software Data Science . Mi próxima publicación actualizará los anuncios de trabajo que listan software científico. Usted también podría estar interesado en mis exámenes a fondo de apuntar y hacer clic  interfaces de usuario a R . Te invito a que te suscribas a  mi blog  o me sigas en  Twitter  donde anuncie nuevas publicaciones. ¡Feliz computación!

AUTOR: BOB MUENCHEN