Presentada por Karl Pearson en 1900, para determinar las diferencias que pueden existir entre observaciones obtenidas en la practica y valores teóricos que le corresponden, se simboliza con la letra griega χ² ,y ademas con el nombre de "Chi Cuadrado". Se aplica para medir la asociación o independencia existente entre dos caracteres o condiciones distintas, observadas en elementos de una misma expresión.
Condiciones para el empleo de la "Chi Cuadrado"
1.- El numero de observaciones no debe inferior a 50, para que se distribuyan normalmente.
2.- Que el numero de observaciones practicas sea igual al numero de observaciones teóricas.
3.- Que la frecuencia de cada clase no debe ser demasiada pequeña, (>= 5), debiéndose agrupar las clases extremas, si es necesario, a fin de obtener como mínimo este limite.
4.- Que su significación este en relación con los grados de libertad de la distribución.
Pasos para calcular la "Chi Cuadrado":
1.- Se hace la diferencia entre cada valor observado y su respectivo valor teórico.
2.- Se eleva al cuadrado esta diferencia.
3.- Se divide cada una de estas diferencias entre su respectivo valor teórico.
4.- Se suman estos coeficientes y se obtiene el valor de la "Chi Cuadrado".
5.- Se calculan los grados de libertad.
6.- Se fija el nivel de significación, luego se compara el valor calculado con el teórico de la tabla correspondiente y se toma la decisión.
En cuanto los grados de libertad, podemos acotar q cuando un estadístico se usa para estimar un parámetro, el numero de grados de libertad disponibles depende de las restricciones impuestas sobre las observaciones, enntonces en la aplicacion de la Chi Cuadrado, existen estas restricciones. Asi tenemos que si un cuadro formado por "c" columnas y "f" filas siendo constantes los valores marginales en uno y otro sentido, el numero de valores independientes de las variables en las cuadriculas en cada fila sera f-1 y en las columnas sera c-1. En conclusión contamos el numero de filas y le restamos una unidad e igualmente contamos el numero de columnas y le restamos una unidad.
el concepto de grados de libertad viene de la física, un cuerpo posee todos sus grados de libertad cuando se encuentra determinado por el largo ancho y el alto, o sea tres dimensiones, pero si realizamos su determinación en función tan solo dos dimensiones, largo y ancho, estamos quitando un grado de libertad, así también, si consideramos los siguientes valores: 2,4, 6, 8, 10, cuya media aritmética es 6 y los desvíos con respecto a dicha media aritmética es -4, -2, 0, 2, 4 de estos desvíos solo N-1, (5) pueden seleccionarse libremente en virtud de que por la primera propiedad de la media aritmética, el sexto esta condicionado a que la suma algebraica de estos desvíos debe ser igual a cero. Para calcular la media aritmética hay N grados de libertad, pero solo (N-1) grados de libertad para determinar la desviación típica.
Ejemplo
Se hizo una encuestas obre 1500 personas en la cual debían expresar su actitud frente a la proposición: ¿Debería Venezuela salir del OEA? La distribución de las respuestas en una escala con 5 opciones se detallan a continuación :
Totalmente Acuerdo Indiferente Desacuerdo Totalmente en
de acuerdo desacuerdo
fo 412 245 327 261 255 1500
ft 300 300 300 300 300 1500
¿Indican estos resultados una tendencia significativa de opinión?
Los valores esperados se calculan partiendo de que las respuestas deberían haberse repartido proporcionalmente entre todas las actitudes.
fo - ft 112 -55 27 -39 -45
(fo -ft)^2 12544 3025 729 1521 2025
(fo - ft)^2
----------- 41,81 10,08 2,43 6,07 6,75
ft
"Chi Cuadrado" = 67,14
Los grados de libertad se obtienen por la formula (c-1)*(f-1) = (5-1)*(2-1) = 4
Para el nivel de significación P= 0,001 y con 4 grados de libertad, se obtiene el valor en la tabla correspondiente igual a 18,465
Dado q el valor de la Chi Cuadrado practica es superior al obtenido en la tabla, debemos rechazar la hipotesis nula de respuestas iguales y concluir que nuestros encuestados favorecen realmente a la proposicion.

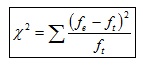
No hay comentarios.:
Publicar un comentario