Contraste de Hipótesis de Diferencias entre Promedios

El problema a resolver es: ¿Cuando podemos decir que la diferencia entre dos promedios es significativa o no?

Cuando esa diferencia sea debida al azar es despreciable y puede considerarse que no hay diferencias significativa, pero en caso de existir una alta diferencia, debido a factores ajenos a los temporarios o accidentales, se considera que tal diferencia es significativa.

Veamos un ejemplo:

En un estudio sobre el rendimiento estudiantil en educación universitaria de tres cursos de Estadística I, se obtuvo el siguiente resultado en una muestra de 70 varones y 65 hembras.

                                                   Nota Promedio               σ              

Varones........................70                13,2                          5,4

Hembras......................65                 14,1                          4,6


Paso 1:

Se formula la hipótesis nula afirmando que no existen diferencias significativas entre los dos promedios.

Suponiendo que estas son tomadas al azar,  ¿Se puede considerar que no existen diferencias significativas entre las notas promedios de las hembras y varones en la población de la cual proceden?

La Hipotesis Nula

Ho: No existen diferencias significativas entre las notas promedios de las hembras y varones 

Paso 2: 

Se fija el nivel de significación, en base al cual se aceptara o negara la hipótesis nula

Los niveles de significación de mayor uso practico son el nivel de 0,00 y el de 0,01

Paso 3:

Se determina el error típico de la diferencia entre dos promedios

Paso 4 y 5:

Se obtiene el valor del Estadístico Z




Paso 6:

Luego este valor es comparado con el valor que se obtiene en la tabla de áreas de la curva normal para niveles de 0,05 y 0,01 los cuales son 1,96 y 2,58 respectivamente. Si Z es mayor e igual a 1,96, se rechaza la hipótesis nula al nivel de 0,05, igualmente es el análisis con el nivel de 0,01


Vamos al ejemplo

Paso 3: Determinaremos el error típico:
                                              ________________________
 σ(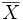1 -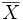2) =        ⬉⬋     (4,6*4,6)/65  +(5,4+5,4)/70  =  0,87


Paso 4: Calculamos la diferencia de los promedios

D = 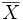1 - 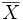2 = 14,1 -13,2 = 0,90

Paso 5: Calculamos el Estadístico

Z = D/(σ(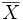1-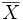2) = 0,90/0,87 = 1,03

Paso 6: Evaluamos la decisión

El valor Z=1,03 , esta por debajo del nivel del valor 1,96 para el nivel de significación de 0,05. De allí que se acepta la hipótesis nula, esto es, que no existen diferencias significativas entre la nota promedio de los varones y hembras, en la población correspondiente.