¿Que es un Factorial?
Es la multiplicación de un numero en forma descendente hasta llegar al 1,
se denota por n!
Ejemplo: 5! = 5*4*3*2*1= 120
Es de resaltar que 1! = 1 y 0! = 1
Ejemplo 2: 5! / 3! = 5*4*3!/3! = 5*4 = 20
Permutaciones:
Las permutaciones son las distintas maneras como pueden ordenarse los diferentes objetos, letras, cosas, etc.
Así, por ejemplo, las permutaciones de dos elementos, a y b, son: ab y ba; las permutaciones de tres elementos a, b y c, son: abc, acb, bca,bac, cab y cba.
Ejemplo: ¿De cuantas maneras se pueden disponer los jugadores de un equipo de Basketball?
Respuesta: El equipo de basketball se compone de 5 jugadores, luego se pueden disponer de P5 = 1*2*3*4*5 = 120 maneras diferentes
La Formula Básica es Pn, r = n!/(n-r)!
Ejemplo 3: ¿De cuantas maneras diferentes se pueden colocarse 8 libros distintos en un estante?
Respuesta:
n = numero de libros = 8,
r = maneras diferentes de colocarse = 8
se sustituye ne la formula P8;8 = 8!/(8-8)! = 8!/0! = 8!/1 = 8*7*6*5*4*3*2*1* = 40320
Ejemplo 4: ¿De Cuantas maneras puede ordenar 4 letras (a,b,c y d) de orden 3?
Respuesta:
n = numero de letras las cuales son 4
r= el orden, es decir, de tres letras
abc acb abd adb acd adc
bac bca bad bda bcd bdc
cab cba cad cda cbd cdb
dab dba dac dca dbc dcb
P4;3 = 4!/(4-3)! = 4!/1! = 4*3*2*1 = 24
Combinaciones:
En las combinaciones, no importa el ordenen que se consideren los elementos, para comprenderlo mejor como se forman las combinaciones, tomemos por ejemplo, cuatro letras a, b , c y d, y escribimos sus combinaciones monarias, binarias y ternarias, entonce resulta:
Las combinaciones monarias son: a, b , c, d
para formar las binarias se agrega sucesivamente a cada monaria las letras que le siguen; se obtiene asi:
ab, ac, ad
bc, bd
cd
Las combinaciones ternarias se obtienen agregando a cada binaria las letras que le siguen en sucesion, una a una; asi resulta:
abc, abd, acd, bcd
La formula de calculo es: Cn;r =n!/r!(n-r)!
Ejemplo hallar el numero de combinaciones de 4 letras de orden 2
Respuesta:
n= numero de letras es 4
r= el orden el cual es 2
sustituyo en la formula:
C4;2 = 4!/2!(4-2)! = 4!/2!*2! = 4*3*2!/2!*2! = 4*3/2! =12/2 = 6


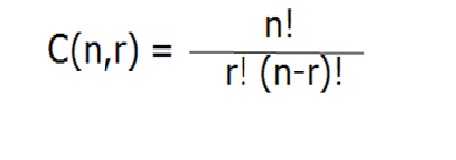
No hay comentarios.:
Publicar un comentario