El Poder de la Tecnología en los Modelos Cuantitativos Lineales y Complejos

Paradojas Probabilística

Probablemente quizás: variación de helado

Escrito por Christoforos Anagnostopoulos y Spiros Doxiadis en 20 marzo 2019. Publicado en Science

. El dicho dice que "las probabilidades son contra-intuitivas". Puede parecer que un problema simple tiene una respuesta directa a primera vista, pero solo luego aprendemos, mediante una explicación cuidadosa, que nuestra intuición ha sido subvertida. De hecho, rara vez se puede confiar en la intuición humana cuando se trata de hacer juicios probabilísticos, especialmente bajo la presión del tiempo. Incluso aquellos capacitados en estadística, como la mayoría de los lectores de Significance , pueden ser víctimas de sesgos cognitivos al tomar decisiones rápidas.

Pero las probabilidades no solo se manifiestan como paradojas. A veces podemos estar intuitivamente en lo cierto sobre un problema que se nos presenta, aunque sea por razones equivocadas o por razones que son difíciles de comprender. Y a veces nos enfrentamos a problemas probabilísticos por los cuales la intuición nos abandona por completo.

Por lo tanto, esta columna se propone ponerlo a usted, el lector, a prueba. Cada vez que presentamos una pregunta para desafiar su instinto probabilístico, junto con la respuesta y algunos comentarios y explicaciones.

Entonces, para comenzar:

El problema
En el pueblo de Chedrok, hay dos vendedores de helados, Dimitrius y Zaza. Dimitrius es un gran trabajador. Él instala su mostrador todos los días temprano en la tarde y no se detiene hasta la mañana siguiente. Atiende a unos 220 clientes por día. Zaza es más relajado. Trabaja solo unas pocas horas por la tarde y rara vez por la noche. Atiende a unos 45 clientes por día.

El abastecimiento de helados es difícil en esta área, por lo que solo venden una cucharada a cada cliente y ambos se conformaron con solo dos sabores, el jengibre y la frambuesa, que son los favoritos de los locales. En general, alrededor del 50% de los clientes eligen la frambuesa. Sin embargo, el porcentaje exacto varía de un día a otro. A veces es superior al 50%, a veces inferior.

Dimitrius y Zaza han tenido una pequeña apuesta entre ellos. Durante un período de tres meses, cada uno registró los días en que más del 60% de sus clientes eligieron el jengibre. Llamaremos a ese día un "día de jengibre".

¿Quién crees que grabó más días de jengibre?

(a) Dimitrius

(b) Zaza

(c) Aproximadamente lo mismo (dentro del 5% del total de cada vendedor)

Lea la descripción nuevamente y tómese un minuto para decidir una respuesta.

La solución

Es habitual que los encuestados salten a (c): cualquier discrepancia entre el número de días de jengibre para Zaza y Dimitrius debería ser pequeña; después de todo, ambos vendedores atienden a la misma audiencia con la misma distribución de gustos. Por lo tanto, cualquier diferencia debe limitarse a pequeñas fluctuaciones aleatorias. Fácil.

Excepto que no es tan fácil. Para ayudar a guiar su intuición, hagamos la pregunta un poco más extrema. Imagine que Dimitrius era en realidad un conglomerado de helados, que atiende a un sorprendente millón de clientes por día. Sería bastante contradictorio para Dimitrius ver que más del 60% de sus clientes eligen jengibre en un día determinado, dada una distribución de sabor igual. Dicho de otro modo, si observara tal eventualidad, probablemente concluiría que la distribución del sabor había cambiado, dada la improbabilidad de la alternativa. Contraste con Zaza, cuyo negocio, en este escenario imaginario, está en tal desorden que solo atiende a cuatro clientes por día. Parece claro que la variación aleatoria tendría un fuerte efecto aquí, y los días de jengibre (y los días de frambuesa también) aparecerían con suficiente frecuencia.

Entonces, menos clientes significa más variabilidad. Más variabilidad significa una mayor probabilidad de que cualquier día dado sea un día de jengibre. Una mayor posibilidad de días de jengibre significa más días de jengibre en cualquier período de tiempo. Entonces, deberías apostar en (b) Zaza.

De hecho, el fenómeno subyacente es ampliamente conocido: a medida que aumenta el tamaño de la muestra, la frecuencia observada de un evento se aproxima a su media real. Las desviaciones de la media son, por lo tanto, mucho más probables para tamaños de muestra pequeños. Pero, incluso si está entre los que eligieron correctamente, aún podría sorprenderse por la velocidad de esta convergencia. En la pregunta original anterior, se espera que aproximadamente 1 de cada 9 días sea un día de jengibre para Zaza, enfrentado a un raro 1 de cada 550 días para Dimitrius. No solo es (b) más probable, es extraordinariamente más probable.

Ahora, imaginemos que le ofrecemos una apuesta: le pagaremos £ 100 si Zaza tiene más días de jengibre en tres meses que Dimitrius, pero debe pagarnos £ 100,000 si no. ¿Tomarías esa apuesta? Es probable que pierda mucho por muy poca ganancia, pero la probabilidad de que gane es 0.9999417. Incluso con la tolerancia del 5% dada en la pregunta, es casi seguro que Zaza tendrá más días de jengibre que Dimitrius. La razón de estas asombrosas probabilidades es que, una vez más, la ley de los grandes números entra en vigencia y la mayor probabilidad de un día de jengibre para los compuestos de Zaza durante más de 90 días, lo que obliga al número promedio de días de jengibre a acercarse a sus valores teóricos esperados: aproximadamente 10 para Zaza, y efectivamente 0 para Dimitrius. Deberías haber tomado esa apuesta.

Hay un nombre en la literatura para este sesgo cognitivo particular: "insensibilidad al tamaño de la muestra" . Lo que es bastante sorprendente, pero también tranquilizador, es que la mayoría de las personas dudarán fácilmente de la precisión de una estadística basada en un tamaño de muestra muy pequeño y, en el extremo, podrían descartarla por completo como anecdótica si se basa solo en uno o dos ejemplos. . Sin embargo, la mayoría de la gente todavía se equivoca con la apuesta de Zaza-Dimitrius: esperan que dos promedios provenientes de muestras de diferentes tamaños de la misma población varíen mucho menos de lo que lo hacen en realidad.

Pero la incertidumbre es variación. Dos lados de la misma moneda.

Hasta la próxima.

Estadísticas en la corte: probabilidades incorrectas !!

Aunque tanto la ley como la teoría estadística tienen fundamentos que se basan en reglas y principios formales, los tribunales pueden aplicar incorrectamente pruebas y argumentos estadísticos. En algunos casos, incluso cuando se llega a una decisión correcta, los tribunales pueden aceptar o dar una explicación que sea inexacta y falsa. En otros casos, el mal uso de las estadísticas ha dado lugar a condenas falsas y años de prisión por delitos no cometidos por el acusado.

La probabilidad plantea un desafío particular para los tribunales. En algunos casos, se han presentado probabilidades incorrectas a los jurados porque se ha utilizado la regla de multiplicación simple, a pesar de que los eventos probablemente no fueron estadísticamente independientes.

La regla de multiplicación para eventos independientes establece que si dos eventos, A y B, son independientes, entonces la probabilidad de que ocurran A y B es la probabilidad de A multiplicada por la probabilidad de B. En notación matemática: P (A y B) = P (A) x P (B). Pero si los eventos no son independientes y se aplica la regla de multiplicación, los resultados pueden ser peligrosamente engañosos, como lo mostrará este artículo.

Nuestro primer ejemplo es de un caso civil que se supone es la primera vez que se presenta evidencia estadística en un tribunal de los Estados Unidos. A continuación, se discutirán cuatro casos penales en los que testigos expertos de la fiscalía utilizaron indebidamente la regla del producto y presentaron probabilidades incorrectas al jurado. En dos de estos casos, un tribunal de apelaciones luego revocó la condena. En los otros dos casos, los acusados ​​colectivamente pasaron 24 años en la cárcel hasta que fueron exonerados por evidencia de ADN.

El Howland falsificará juicio

En 1868, la voluntad de Sylvia Ann Howland fue objeto de una batalla legal. Había dejado aproximadamente la mitad de su fortuna a su sobrina, Henrietta Howland Robinson. Sin embargo, Robinson afirmó que un testamento diferente le dejó todo el patrimonio. El abogado del patrimonio argumentó que la firma en el testamento que Robinson prefería era una falsificación, por lo que el abogado de Robinson le pidió a Oliver Wendell Holmes, Sr., profesor de anatomía y fisiología en Harvard, que testificara sobre la autenticidad de la firma. Examinó la firma bajo un microscopio y no encontró evidencia de falsificación.

El abogado de la finca llamó a Benjamin Peirce, profesor de matemáticas en Harvard, para testificar. Peirce utilizó técnicas estadísticas para decidir si la firma era "demasiado similar" a otra firma conocida de Sylvia Howland. Llegó a la conclusión de que "la probabilidad de encontrar 30 coincidencias de carrera descendente en un par de firmas fue una vez en 2,666 millones de millones de millones".

Perfore las probabilidades asignadas para cada una de las 30 similitudes y luego multiplique para llegar a la probabilidad final, extremadamente pequeña. Sin embargo, en un artículo de 1980, Paul Meier y Sandy Zabel hicieron una excepción a este cálculo.1 Discuten el "uso y abuso de la regla del producto para multiplicar las probabilidades de eventos independientes". Argumentan que los 30 eventos / similitudes separados probablemente no sean independientes.

El tribunal finalmente decidió este caso contra Robinson en un punto legal separado, no sobre si el testamento era una falsificación.

El juicio de Malcolm Collins

Se dice que hay dos tipos de estadísticas: las que buscas y las que inventas. El caso de People v. Collins contiene ejemplos de esto último.

El acusado, Malcolm Ricardo Collins, fue acusado de robo y condenado. La condena fue apelada ante la Corte Suprema de California . La siguiente evidencia fue presentada en el ensayo original.

A una mujer le robaron el bolso. Los testigos no pudieron ver bien la cara del ladrón; sin embargo, los testigos pudieron describir algunas características del ladrón (una mujer blanca con una cola de caballo rubia), el auto de escape (un vehículo amarillo) y el conductor (un hombre negro con barba y bigote). En el juicio, la fiscalía llamó a un instructor de matemáticas para testificar. El instructor explicó la regla del producto para multiplicar las probabilidades de eventos independientes. La fiscalía sugirió las siguientes probabilidades al instructor: hombre negro con barba, 1 de cada 10; hombre con bigote, 1 de cada 4; mujer blanca con cola de caballo, 1 de cada 10; mujer blanca con cabello rubio, 1 de cada 3; automóvil amarillo, 1 de cada 10; y una pareja interracial en auto, 1 de cada 1,000. Le preguntó al instructor cuál sería la probabilidad de que estos eventos ocurrieran simultáneamente, usando estas estimaciones, y el instructor dio la respuesta: 1 en 12,000,000. El fiscal afirmó que estas estimaciones eran conservadoras y que la probabilidad real era más cercana a 1 en mil millones.

El jurado declaró culpable a Collins, pero el fallo de la corte de apelaciones señaló: "Es una circunstancia curiosa de esta aventura como prueba de que el fiscal no solo hizo sus propias afirmaciones de estos factores con la esperanza de que fueran conservadores ... sino que invitó al jurado para sustituir sus estimaciones ". El tribunal continuó:" Hubo otro defecto evidente en la técnica de la fiscalía, a saber, una prueba inadecuada de la independencia estadística de los seis factores ".

Por ejemplo, la probabilidad de que un hombre con barba no sea independiente del hombre que tiene bigote. Además, ¿no se tendría ya en cuenta el hecho de que una pareja interracial estaba en el automóvil, dado que el presunto ladrón era una mujer blanca y se decía que el hombre que conducía el auto de escape era negro? La decisión final de la corte de apelaciones fue: “Las matemáticas, un verdadero hechicero en nuestro mundo computarizado, mientras ayudan al juzgador de hecho en la búsqueda de la verdad, no deben hechizarlo. Revertimos el juicio ".

Desafortunadamente, la explicación de la falta de independencia de la corte de apelaciones en el caso Collins es incorrecta. La corte declara que los eventos "los hombres negros con barba y los hombres con bigote representan categorías superpuestas". Si bien esta afirmación es cierta, no es la razón por la cual los eventos no son independientes. Colin Aitken, en su libro Estadística y evaluación de la evidencia para científicos forenses., da la explicación correcta: “El testimonio estadístico carecía de una base adecuada tanto en evidencia como en teoría estadística. ... La primera razón se refiere a la falta de justificación ofrecida para la elección de los valores de probabilidad y la suposición de que las diversas características eran independientes. Como ejemplo de este último punto, una suposición de independencia supone que la propensión de un hombre a tener bigote no afecta su propensión a tener barba ”.2

El hecho de que los hombres negros con barba y los hombres con bigote sean categorías superpuestas no es la razón por la cual estas categorías no son independientes.

El juicio de Sally Clark

Sally Clark era abogada en Cheshire, Inglaterra.3 Su hijo, Harry, nacido tres semanas antes de tiempo, murió ocho semanas después del nacimiento, y ella fue acusada de su asesinato. Su primer hijo también había muerto, menos de tres semanas después del nacimiento, y aunque su autopsia concluyó que había muerto por causas naturales, Clark también fue acusado de asesinarlo. Fue arrestada y acusada, a pesar de que había poca evidencia en su contra.

En el juicio de Clark, Sir Roy Meadow, pediatra, dio testimonio estadístico. Afirmó que la probabilidad de que un bebé aleatorio muera de muerte súbita (SMSL) si la madre es mayor de 26 años, rica y no fumadora, es de 1 en 8,543, y por lo tanto, la probabilidad de que dos hijos de una familia así tengan una muerte súbita es (1 en 8,543) x (1 en 8,543) = 1 probabilidad en 73 millones. El resumen del juez al jurado incluyó la declaración: "Aunque no condenamos a las personas en estos tribunales por estadísticas ... las estadísticas en este caso son convincentes". Después de su condena, un miembro del jurado dijo: "Lo que usted diga sobre Sally Clark, puede" evite la cifra de 1 en 73 millones ”. La condena de Clark fue confirmada en apelación.

En 2001, la Royal Statistical Society emitió un resumen de noticias condenando el uso de la regla de multiplicación para la independencia en este caso, afirmando que: “Este enfoque es estadísticamente inválido. … La cifra bien publicitada de 1 en 73 millones no tiene base estadística ”. En 2002, Ray Hill, profesor de matemáticas en la Universidad de Salford, analizó otros datos publicados. Llegó a la conclusión de que la probabilidad de que un segundo hijo muera por una muerte en la cuna, dado que el primer hijo tuvo una muerte en la cuna, puede ser tan alta como 1 en 60. En 2003, después de pasar tres años en la cárcel, se confirmó la segunda apelación de Clark, y ella fue liberada de la cárcel. Esto fue solo después de que un nuevo abogado pro bono, mientras revisaba la evidencia, descubriera un informe de patología que revelaba que Harry estaba infectado con Staphylococcus aureus, y que este hecho había sido ocultado a su equipo de defensa.

Sally Clark murió en 2007.

El juicio de Jimmy Ray Bromgard

En 2015, la Oficina Federal de Investigaciones admitió que durante más de 20 años su personal de laboratorio forense había dado un testimonio erróneo en juicios penales que incluían análisis microscópico del cabello.4 En muchos casos, afirmarían que la probabilidad de que un cabello del cuero cabelludo dejado en la escena del crimen coincida al azar con el cabello del acusado fue de 1 en 4.500. Para un vello púbico, la probabilidad era de 1 en 800. Estas probabilidades se derivaron de un estudio defectuoso de Gaudette y Keeping.5 5

En el juicio de 1987 de Jimmy Ray Bromgard, sobre la violación de una niña de ocho años, el experto forense del fiscal testificó que encontró una coincidencia entre el cuero cabelludo del acusado y el vello púbico de la escena del crimen. Sin ofrecer una base, afirmó que la probabilidad de una coincidencia para el cabello del cuero cabelludo era de 1 en 100 y para el vello púbico también era de 1 en 100. Opinaba que, dado que los pelos eran de diferentes partes del cuerpo, estas coincidencias eran independientes. Luego, utilizando la regla de multiplicación para eventos independientes, llegó a la conclusión de que la posibilidad de que el cabello fuera de otra persona que no fuera el acusado era de 1 en 10,000.

Como en otros casos donde la regla de multiplicación fue mal utilizada, el testigo experto multiplicó las probabilidades (para obtener una probabilidad mucho menor) sin presentar ninguna evidencia de que los eventos son independientes. De hecho, el cabello del cuero cabelludo y el vello púbico de una persona tienen similitudes (por ejemplo, color, textura cortical), en cuyo caso una coincidencia en el cabello del cuero cabelludo no sería independiente de una coincidencia en el vello púbico.

Bromgard fue condenado y pasó 14 años en la cárcel hasta que las pruebas de ADN demostraron que no cometió el asalto. Setenta y tres individuos más, condenados principalmente por análisis microscópico del cabello, fueron exonerados por evidencia de ADN, pero solo después de pasar 1.056 años colectivos en la cárcel.

El juicio de Ray Krone

Ray Krone fue condenado por asesinar a un cantinero en 1992. La principal evidencia forense presentada en el juicio fue una marca de mordisco en el cuerpo del cantinero que se suponía que había sido dejado por el asesino. Raymond Rawson, un dentista forense, testificó que la marca de la mordida en el cuerpo no solo coincidía con la dentición de Krone, sino que solo podía provenir de Krone.

Rawson basó su conclusión en un estudio que publicó en 1984, "Evidencia estadística de la individualidad de la dentición humana".6 El estudio afirmó que la dentición humana es única; sin embargo, el estudio tenía varios defectos que hicieron insostenible esta afirmación. Nuestro artículo anterior tiene más detalles, pero el problema básico es el siguiente: Rawson y sus colegas utilizaron impresiones dentales de cera de una muestra de conveniencia de 1,200 sujetos para calcular el número total de posiciones únicas de cada uno de los 12 dientes: seis de la mandíbula superior, seis de la mandíbula inferior Luego calcularon el producto del número de posiciones para los dientes superiores e inferiores, y ambos se unieron, llegando a un número mayor de cuatro mil millones para el número total de posiciones únicas para la dentición humana, que era más que todas las personas en la Tierra En ese tiempo.

Como escribimos en 2016: “[T] su cálculo solo es válido si los datos son independientes. Sin embargo, parecería obvio que la posición de un diente estaría influenciada por las posiciones de los dientes que lo rodean. Por lo tanto, la regla del producto no se aplica para determinar el número total de puestos únicos para denticiones humanas ".

Krone pasó 10 años en la cárcel antes de ser liberado, luego de que pruebas de ADN demostraran que no era el asesino. Al menos otras veintitrés personas, condenadas principalmente por análisis de marcas de mordisco, han sido exoneradas de manera similar.

Resumiendo

En los juicios penales, especialmente aquellos que involucran análisis microscópico del cabello y comparaciones de marcas de mordida en humanos, se presentaron al jurado probabilidades incorrectas. En muchos casos, las probabilidades se multiplicaron juntas independientemente de si los eventos eran independientes.

Con respecto a este problema de falta de independencia, el tribunal de apelaciones en el caso de Malcolm Collins dijo: "Se podría esperar que pocos abogados defensores, y ciertamente pocos miembros del jurado, comprendan este defecto básico en el análisis de la fiscalía". Sin embargo, los estadísticos lo entienden, y la justicia puede estarían mejor atendidos si se les pidiera que revisaran los cálculos antes del juicio.

---

Sobre el Autor

H. James (Jim) Norton es profesor emérito de bioestadística, Carolinas HealthCare System, Charlotte, Carolina del Norte. Ha sido testigo experto o consultor en ocho casos legales, incluidos seis que involucraron evidencia forense. Su sitio web es jimnortonphd.com . George Divine es bioestadista de investigación sénior en el Hospital Henry Ford, Detroit, Michigan.

El primer planeta más allá del sistema solar confirmó tener agua

 Desde su descubrimiento por los astrónomos en 2015, el exoplaneta k2- 18b ha suscitado mucho entusiasmo. Girando alrededor de una estrella enana roja a unos 110 años luz de distancia de la Tierra, el mundo distante se encuentra en una zona llamada Ricitos de Oro, no lo suficientemente cerca de su estrella anfitriona como para estar demasiado caliente y no lo suficientemente lejos para estar demasiado frío. podría permitir que el agua líquida fluya a través de su superficie. Esa es una condición crucial para la vida tal como la conocemos.

Ahora los astrónomos han aumentado la especulación. Las imágenes de seguimiento tomadas por el Telescopio Espacial Hubble sugieren que k2-18b (la impresión del artista a continuación) tiene una atmósfera que contiene grandes cantidades de vapor de agua, el primer exoplaneta en una zona habitable que lo confirmó. La mayoría de los exoplanetas encontrados previamente con atmósferas han sido gigantes gaseosos, similares a Neptuno o Júpiter. en cambio, K2-18b parece que podría ser un planeta rocoso dos veces más grande que la Tierra, tal vez cubierto de vastos mares cubiertos de hielo.

Fuente: The Economist

Edición impresa | Ciencia y Tecnología

12 de septiembre de 2019

Introducción a HTML

Contraste de Hipótesis de una Media

El Contraste de Hipótesis es una técnica estadística, que trata de comprobar  los resultados de una Suposición, Afirmación, Postulado o Enunciado que realicemos mediante una oración gramatical, conjetura o propuesta, de gran importancia, que sirva para el proyecto, investigación, experimento o estudio, en cualquier área.

Ejemplo de Hipótesis:

a.- El Administrador de un Hospital afirma que desea estudiar, la duración media de pacientes internados es menor a cinco días.

b.- Una Empresa espera que por termino medio un caucho dure 600 días, en condiciones normales.

c.- Un fabricante supone que su producto tenga un contenido promedio de 120 grs.

d.- Un fabricante  produce baterías, cuya duración debe ser menor a 2 años.

e.- Se supone que una lata de atún,  tiene un costo promedio de 10 Bs.

f.- En cada partido de fútbol, el amigo Pepito nos afirma que el mete 2 a 3 goles.

g.- Andrew afirma que en un partido de béisbol, de cada cuatro turnos al bate el da 3 hit.

h.- Diego supone que para captar mas clientes debe realizarse 5 comerciales diarios en tv.

i.- Augusto en el área de Odontología, me comenta que el número promedio de pacientes que atiende en verano es de 60.

Hay tres conceptos que debemos mencionar, ya que se utilizan en la elaboración de los contrastes de hipótesis:

Parámetro: es una constante asociada a una distribución probabilista, ejemplo en la Distribución Normal los parámetros son u y σ.


Estimador: es un estadístico que toma valores cercanos al verdadero valor del parámetro, ejemplo la media aritmética y la desviación estándar o típica (σ).

Estadístico: Es una variable aleatoria en función de las observaciones muestrales.

Otra definición importante que conviene aclarar, es la considerar como "muestra grandes"  aquella cuyo valor de "n" sean mayores e iguales a treinta (30); para menores de treinta (30) se consideran " muestras pequeñas".

Al tomar una muestra y determinar sus estadísticos, se debe inferir  o estimar los parámetros del grupo a estudiar, del cuál procede, lógicamente el valor de estos estadísticos no será exactamente el valor de los parámetros, estos se encontrarán afectados por las llamadas fluctuaciones de la muestra. Sin embargo, siempre los métodos estadísticos irán encaminados a predecir  con un alto grado de exactitud  los parámetros del grupo a estudiar, en función de los estadísticos tomados de la muestra.

El grado de exactitud es el llamado Nivel de Significación.

Se expresa en general por su error típico, cuya significación es la misma que la desviación típica, este nivel representa la probabilidad de rechazar una hipótesis

Cuando se use una muestra de tamaño grande (30 o más), la distribución de resultados muestrales se aproximara a la distribución normal ( figura anterior), llamada Curva Normal o de Gauss, es decir, se expresa que existe una probabilidad del 68,2% que el valor del parámetro se encuentra entre los limites determinados por la constante estadística calculada y mas o menos su error típico (σ); también se puede expresar del 95,8% que se encuentre la constante estadística y mas o menos 2 veces su error típico.
Estos limites son de  fundamental importancia para la significación muestral, así, que suponiendo extraemos, de una población una muestra aleatoria simple y calculamos su promedio y su error típico. La pegunta será Cómo podemos inferir la precisión de este resultado muestral en particular?

Para ello se debe determinar un intervalo de la estimación muestral, entonces podemos con bastante confianza afirmar que (X -σ< X < X + σ) será un intervalo tal, que en dos tercios  de los casos resultará correcto asumir que el valor verdadero de la media cae dentro de ese intervalo. En forma similar, (X +- σ) nos dara un intervalo para que la suposición sea correcta en el 95,8% de las veces .

Ejemplo: El dueño de un negocio de ventas de cerveza, desea saber si la edad promedio de las personas que entran a su local es de 20 años. Si eso es verdad se piensa realizar una remodelación acorde al nicho de mercado existente, para hacerlo mas juvenil, atractivo y que mejore las ganancias.

Para ello se realiza un muestreo aleatorio de 40 personas,dando un promedio de la muestra de 22 años y una desviación típica de 3,74 años.

Ahora realizaremos un Contraste de Hipótesis de Media

Paso 1: Determinar la Hipótesis Nula (Ho) y la Hipótesis Alternativa (H1)

Ho: La edad promedio de los clientes que entran al negocio es igual a 20 años

Ho = 20

H1: La edad promedio de los clientes que entran al negocio es diferente  a 20 años

H1: =/20

Paso 2: Determinar el Nivel de Significación

Este nivel representa la probabilidad de rechazar una hipótesis nula verdadera

Sus niveles serán de α = 0,1 α= 0,05

¿Qué significa esos niveles de donde se los sacan?

Estos niveles son los más frecuentes y utilizados, cuando decimos un α = 0,1  significa que en porcentaje estamos diciendo que tenemos un 90% de confianza, y del 0,05 decimos que es del 95% de confianza.

Con estos niveles nos ubicamos en la tabla de la normal y buscamos el valor asociado a Z

Si seleccionamos α=0,1 esto implica en porcentaje 10%, entonces la diferencia de  10% a 100% es 90%, este valor le convertimos en numero y nos da 0,90, luego buscamos este valor en la tabla de la distribución normal, ahí tenemos que como la curva es simétrica  la mitad es 0,45, al ubicar este valor en la tabla nos da que el valor de Z es 1,64, tal como lo señala en roja el cuadro anterior.

Si selecciono el 0,05 de nivel de significación, Cuál seria el valor en la tabla ?

La respuesta es 1,96

Hay una forma fácil de obtener estos valores en el paquete computacional de excel que incorpora windows,  Colocaremos la siguiente función:     @Distr.norm.estand.inv(90%+0,1/2)

y el resultado será de 1,64

Se recomienda probar con el nivel de significación del 0,05


Paso 3: Calcular los Intervalos que implican ese nivel de significación

Nivel de Confianza = 90%

Z = 1,64

Intervalo de confianza [ -1,64 < x < 1,64]

Paso 4: Calcular el Estadístico de la Prueba de Media

Datos

μ = 20

x = 22

σ = 3,74

n= 40

Al calcular el Z nos da un valor de 3,38212

Paso 5: El estadístico cae en la región de aceptación

el valor -1,64 y 1,64 se encuentra donde esta señalizado -Zo y Zo, dentro de esos dos valores es la zona de aceptación de la hipótesis, como observamos el Estadístico Z = 3,38212 esta en la zona negra de la gráfica o zona critica, este valor es mayor el 1,64


Paso 6: Aceptamos o rechazamos Ho?


Se RECHAZA la Hipótesis Nula  y se ACEPTA la Hipótesis Alternativa

En excel es muy fácil de elaborar

Alguna  pregunta escriban a mi correo: zavafree@gmail.com, con gusto, aclararemos las dudas.

Contraste de Wilcoxon para muestras apareadas

El contraste de Wilcoxon es la técnica no paramétrica paralela a el de la T de Student para muestras apareadas . Igualmente dispondríamos de n parejas de valores (x_i,y_i) que podemos considerar como una variable medida en cada sujeto en dos momentos diferentes.

  Para todo i = 1,2,....,n,        i-ésima oservación = (Xi,Yi)----> diferencia = Di =Xi - Yi

El test de Wilcoxon, al igual que los otros contrastes no paramétricos puede realizarse siempre que lo sea su homólogo paramétrico, con el inconveniente de que este último detecta diferencias significativas en un 95% de casos que el de la T de Student.
Sin embargo a veces las hipótesis necesarias para el test paramétrico (normalidad de las diferencias apareadas, d_i) no se verifican y es estrictamente necesario realizar el contraste que presentamos aquí. Un caso muy claro de no normalidad es cuando los datos pertenecen a una escala ordinal.
El procedimiento consiste en:

1.

Ordenar las cantidades ! Di ! de menor a mayor y obtener sus rangos.

2.

Consideramos las diferencias d_i cuyo signo (positivo o negativo) tiene menor frecuencia (no consideramos las cantidades d_i=0) y calculamos su suma,                                                                             T   sera:  Si Di >0             si los signos positivos de Di son menos frecuentes                                                                                                                                                                                                         Si  Di< 0              si los signos negativos de Di son menos frecuentes

Del mismo modo es necesario calcular la cantidad T', suma de los rangos de las observaciones con signo de d_i de mayor frecuencia, pero si hemos ya calculado T, la siguiente expresión de T' es más sencilla de usar   T = m(n + 1) -T

donde m es el número de rangos con signo de d_i de menor frecuencia.

3.

Si T ó T' es menor o igual que las cantidades que aparecen en la tabla de Wilcoxon, se rechaza la hipótesis nula del contraste                                                                           

     H0 : No hay diferencia entre observaciones apareadas                                                                                                                                                                                                                       H1: Si la Hay

 Aproximación normal en el contraste de Wilcoxon

Si n>= 100 la distribución de T admite una aproximación normal

                                                        T = N(ut,st)

donde 

la Esperanza matemática es:     ut = n(n+1)/4

La Varianza  es                         st =n(n+1)(2n+1)/24

por lo que el estadístico 

Z = T -ut/(st)^1/2      la cual es una aproximación a la Normal (0,1)

da como criterio el rechazar       H0   si  |Z| >= 1- alfa/2

Histograma? Qué es y como elaborarlo

Los histogramas son una forma de resumir una variable numérica continua. Se usan para  mostrar la distribución general. Sin embargo, pueden ser sensibles a las opciones de parámetros! Vamos a llevarlo paso a paso a través de las consideraciones con muchas visualizaciones de datos. Si hay algo que no entienda después de leer el ensayo, puede contactarnos; Nuestra información de contacto está al final y en el perfil del blog. ¡Comentarios y sugerencias son bienvenidos!

Al recolectar los datos,  de una sola variable, lo primero es pensar como lo vamos  a ordenar y a clasificar,  nos centramos, en la forma de visualizar  una distribución, ella  depende de si la variable de interés es categórica o numérica, es decir, si la variable es cualitativa,  cuantitativa  discreta o cuantitativa  continua.

Variables categóricas o cualitativas y sus distribuciones.

Las variables categóricas toman solo unos pocos valores específicos. Por ejemplo, el género es una variable categórica común, quizás con las categorías "masculino", "femenino" y "no conforme con el género".

Para visualizar la distribución de una variable categórica, usamos lo que se llama un gráfico de barras, estos muestran cuántos elementos se cuentan en cada conjunto de categorías. Por ejemplo, el siguiente gráfico de barras se realizó con la finalidad de ver gráficamente cuantos estudiantes o alumnos realizan  cursos en la academia fz .

 Es una variable cualitativa nominal, donde se cuenta  cuántas personas hay en cada curso de programación.

Debido a su naturaleza discreta, no hay mucho que decidir al dibujar un gráfico de barras. Un analista puede elegir el orden de las categorías, el color de las barras y la relación de aspecto, para visualizar dicho información.

Variables numéricas (Cuantitativas Discreta o Continua) y sus distribuciones.

Las variables numéricas se miden como números. La altura es numérica, a menudo se mide en centímetros o pulgadas. La edad es numérica, medida en años o días. Las variables numéricas pueden ser discretas o continuas . Las variables discretas solo toman valores enteros (1, 2, 3, etc.). Las variables continuas toman cualquier valor a lo largo de la línea numérica o el conjunto de números reales (1.7, 14.06, etc.).

Cuando una variable es numérica, su distribución se puede representar de varias maneras ; Probablemente el método más común es el histograma.

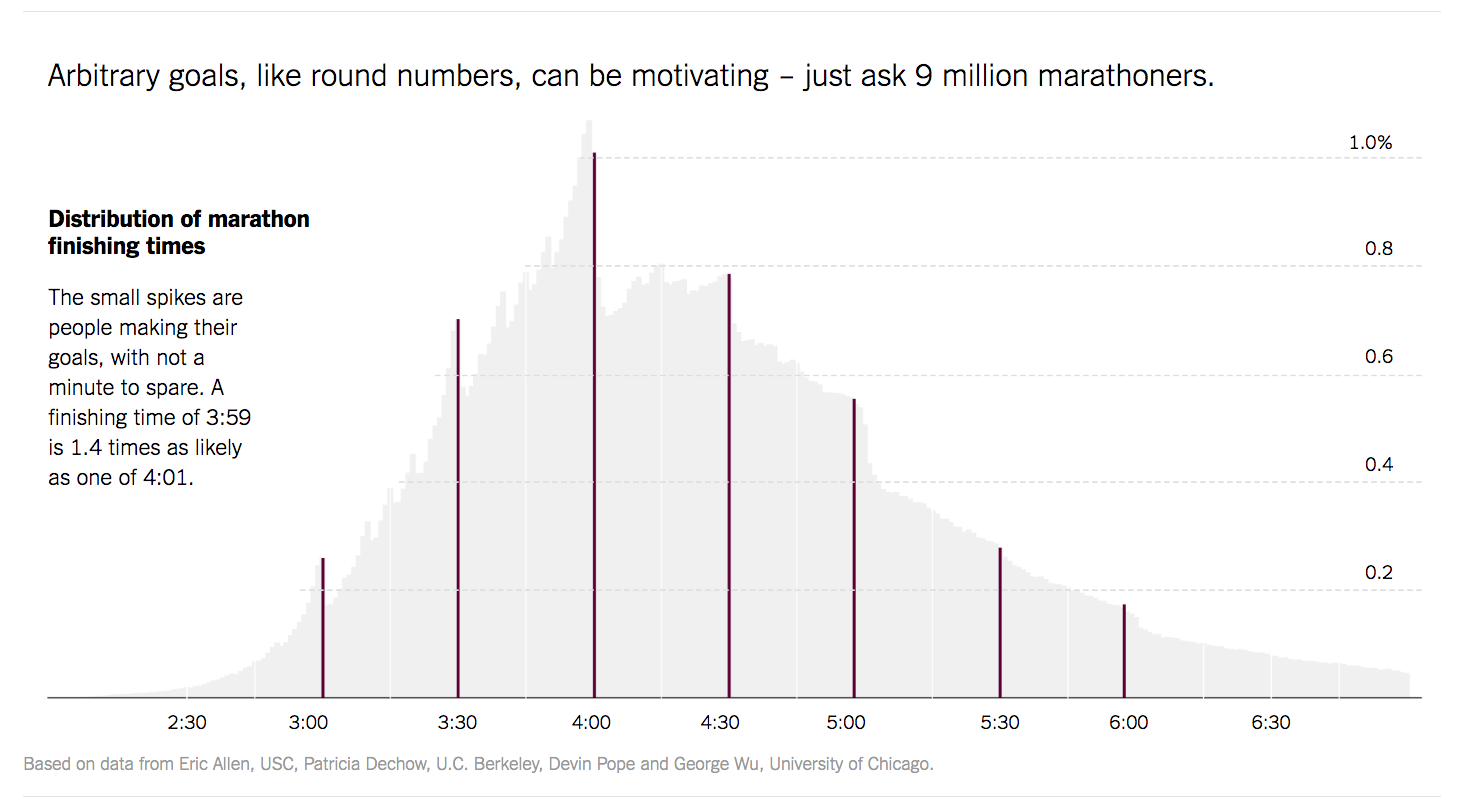
Justin Wolfers de The Upshot produjo el histograma de la siguiente figura para visualizar los tiempos finales de 10 millones de corredores de una maratón.

A primera vista, la creación de un histograma parece bastante simple: dividimos los datos en un conjunto de contenedores, cajas o grupos, discretos, luego contamos cuántos valores caen en cada uno de los grupos. Pero, al observar más detenidamente, vemos que en realidad hay muchas opciones que se deben tomar para crear un histograma que represente fielmente la forma de la distribución.

Cómo construir un histograma

Reúne tus datos

Un histograma se basa en una recopilación de datos sobre una variable numérica. Nuestro primer paso es reunir algunos valores para esa variable.  Podemos visualizar el conjunto de datos como un conjunto de elementos, con cada elemento identificado por su valor, que en teoría nos permite "ver" todos los elementos, pero hace que sea difícil obtener un comportamiento de la variable. ¿Cuáles son algunos valores comunes? ¿Hay mucha variación?

Ordenar en una lista 

Un primer paso útil para describir la distribución de la variable es ordenar los elementos en una lista. Ahora podemos ver el valor máximo y el valor mínimo. Más allá de eso, es difícil decir mucho sobre el centro, la forma y la distribución de la distribución. Parte del problema es que la lista está completamente llena; el espacio entre dos elementos es el mismo, sin importar cuán diferentes sean sus valores. Necesitamos una forma de ver cómo los elementos se relacionan entre sí. ¿Están agrupados alrededor de unos pocos valores específicos? ¿Hay un objeto solitario con un valor muy alejado de todos los demás?

Construye la Distribución de Frecuencias

Obtén el Rango, ======>>>>>      Rango = Valor Mayor - Valor Menor, esto es para determinar el intervalo total, donde estarán comprendidos todos los valores de la serie de datos a estudiar.

Luego tienes que decidir el número de intervalos de clases a realizar, no hay reglas para esta decisión, todos los métodos existentes son empíricos, según las bibliografias de Estadísticas mas famosas en el tema. Se recomienda hacer distribuciones de frecuencias que tengan mínimo cuatro (4) intervalos de clases, máximo siete (7), ya que su visualización es aceptada en la mayoría de los casos. Los intervalos de clases deben ser, siempre que sea posible, iguales, a fin de de que la comparabilidad entre las frecuencias de las diversas clases se torne fácil. El intervalo de clase no debe ser tan grande que oculte las características más importantes de la variable a estudiar.

luego de obtener el Rango y el Número de Intervalos. se realiza el cálculo del Tamaño de cada Intervalo o intervalo de Clases.

Rango = (VM - Vm) ;       NI =Número de Intervalos

Tamaño del Intervalo =Rango/Número de Intervalos

Un procedimiento alternativo para determinar el intervalo de clase o tamaño del intervalo, ha sido sugerido por H.A. Sturges, aplicando la siguiente fórmula:

Tamaño del Intervalo = Rango/( 1+3,322*log(N))

Esta fórmula da valores fraccionarios no adecuados para su uso en la práctica; sin embargo, podemos aplicar las reglas de redondeo y convertirlos en enteros o eliminar algunos decimales en cuanto sea posible. 

Es importante indicar con precisión los limites de las clases y evitar clasificaciones como estas:

0--------10
10------20
20------30

como se observa los valores 10 y 20 pertenecen a dos clases, los cuales cuando estemos registrando las frecuencias se realizarían dobles. Tampoco se debe escribir: 

más de  0   menos de 10
más de 10  menos de 20

ya que el valor de 10 no pertenece a ninguna de las  clases citadas.

Una forma de presentación de clases que  se sugiere es:
 0-----9,9
10---19,9 
20---29,9
30---40
la cual no presenta los vicios señalados anteriormente

otra clasificación correcta es para variables discretas
10------19
20------29
30------39
40------49
50------59

Una vez , construidos los intervalos de clases, registramos la frecuencia que tiene los datos de la variable a estudiar, en cada uno de los intervalos de clases, ya una vez  obtenida la distribución de frecuencias, se dibuja los ejes de coordenadas sobre el plano

En el eje de las abscisas (x), se coloca los intervalos de clases y sobre el eje de las ordenadas la magnitud de cada frecuencia,  luego se levantan rectángulos o barras en cada clase formada.

En el caso del maratón, por ejemplo,  el tiempo mínimo fue 2 horas, y el tiempo máximo de los maratonista fue de 5 horas.

Hallamos el rango. Rango = 5-2 = 3

Luego decidimos que el número de intervalos es 6.

Hallamos el Tamaño de cada intervalos es Ic = 3/6 = 1/2 =0.5

Construimos la Distribución de Frecuencias

             Distribución de frecuencia
Se escribe la variable          Frecuencia
                       ↓                           ↓
Tiempo en horas y minutos N° de personas
2,00 ------------------2,5                  99
2,501-----------------3,0                201
3,001-----------------3,5                450
3,501-----------------4,0                350
4,001-----------------4,5                188
4,501-----------------5,0                112
Total                                       1400

En excel sería  así:

La Gráfica o Histograma, del lado del eje de las ordenadas, se levanta la columna del N° de personas, y del lado del eje de las abscisas, se construyen los intervalos de clases, en este caso: las horas del tiempo de la maratón, las cuales fueron agrupadas por cada media hora.

Preguntas : Porqué se seleccionó 6 intervalos de clases?

Cuál es la distribución de los datos? 

Los histogramas proporcionan una forma de visualizar datos agregándolos en barras, y se pueden utilizar con datos de cualquier tamaño.

La división de elementos en las barras: la esencia de un histograma

Reunir los datos en barras nos ayuda a responder la pregunta "¿Cómo es la distribución de estos datos?" Imagine, que ud. intenta describir algunos conjuntos de datos, que le están comunicando por teléfono, en lugar de leer mecánicamente toda la lista de valores, sería más útil proporcionar un resumen, como para poder decir, si la distribución de la variable es simétrica, dónde está centrada y si tiene valores extremos, etc. Un histograma es otro tipo de resumen, en el que se comunican las propiedades generales en términos de porciones (es decir, barras) de los datos

Tal vez porque los histogramas son visualmente similares a los gráficos de barras, es fácil pensar que también son objetivos similares. Pero, a diferencia de los gráficos de barras, los histogramas se rigen por que se visualizan las variables cuantitativas continuas, donde un intervalo tiene inmediatamente la secuencia del otro en términos de números reales.Además, podemos señalar que antes de describir un conjunto de datos a alguien, en función de lo que ve en su histograma, debe saber si los diferentes valores de los parámetros podrían haberlo llevado a diferentes descripciones.

Lo importante es que un histograma,  es un resumen representativo de un conjunto de datos subyacente.

En la figura del histograma anterior que se puede visualizar? Cual es el comportamiento de la variable? Que podemos decir de los datos?  Se observa la data o distribución simétrica? Que conclusiones podemos sacar de la gráfica? 

Con este pequeño ejemplo, espero haber ayudado un poco a resolver la construcción del Histograma, si tienes alguna duda, deja tu comentario o escribe al correo zavafree@gmail.com que con gusto trataré de aclarar las dudas.