Determinación del tamaño de muestra para estimar medias poblacionales

La pregunta es: ¿que tan grande debemos seleccionar el tamaño de muestra para una investigación o un experimento?

"Esto es importante y no debe de tratarse con ligereza", porque tomar una muestra más grande  de lo necesario para alcanzar los resultados deseados, es un desperdicio de los recursos, tanto en costo y tiempo de la investigación, y si tenemos muestras pequeñas con frecuencia conducen a resultados sin uso práctico. Entonces, el tamaño de la muestra depende de la Desviación Estándar de la Población, el Grado de Confiabilidad o Nivel de Significación y el Error Estándar o Deseado
La fórmula para el cálculo de la muestra es:



                                                                       no
                                                                     n =     ---------            (1)
                                                                   1  +  no
                                                                                                                 N

donde:

                                                      2           2
                                               Z    S 
                                   no = ----------------                           (2)
                                                     2
                                               e 

Z= Nivel de significación

S= Desviación estándar

e= Error de medición estándar

El tamaño de la muestra requiere que se conozca la desviación estándar, pero generalmente se desconoce. Como resultado, tiene que estimarse. Las fuentes de estimaciones que se usan con mas frecuencia son las siguientes:

1.- Puede extraerse una muestra piloto o preliminar de la población y puede usarse la varianza calculada a partir de esta muestra como una estimación de    .

2.- Puede obtenerse con estimaciones obtenidas de estudios anteriores.

3.- Si se tiene la sensación de que la población de la cual se va a extraer la muestra está distribuida aproximadamente en forma normal, puede usarse el hecho de que el recorrido es aproximadamente igual a seis desviaciones estándar y calcular S=R/6. Este método requiere de cierto conocimiento del valor máximo y mínimo de la variable a estudiar de la población.

Ejemplo 1.

Mi amiga Veruska, nutrióloga  de salud de un Hospital de la Ciudad de Caracas, desea conducir una investigación entre una población de muchachas adolescentes, con el fin de determinar su ingestión diaria promedio de proteínas, está buscando el consejo de un estadístico, relativo al tamaño e muestra que debe tomar.

¿qué procedimiento sigue el estadístico para proporcionar asistencia a la nutrióloga ?

Antes que el estadístico pueda ayudar a Veruska,  ésta debe dar tres detalles de información:

a.- el ancho deseado del intervalo de confianza,

b.- el nivel de confianza deseado, y

c.- la magnitud de la varianza de la población.

Supongamos que a la nutrióloga le gustaría un intervalo de 10 unidades de ancho, es decir, le gustaría que su estimación de error deseado estuviera dentro de cinco unidades aproximadamente de la verdadera, en cualquier dirección. Supongamos también que se decide por nivel de confianza del 95% y que, de su experiencia pasada, la nutrióloga siente que la desviación estándar de la población es probablemente alrededor de 20 gramos. Ahora el estadístico tiene la información necesaria para calcular el tamaño de muestra.

Datos:

Nivel de confianza de  95% , quiere decir,  que este dato lo llevamos a la tabla de la curva de la normal y equivale a Z = 1,96

Error estándar = 5, ya que ella quiere que su intervalo de confianza sea + o - igual a 5 del promedio aritmético.

Y la Desviación estándar  o variabilidad de sus datos es de 20 gramos.

Supongamos que la población de interés es grande de modo que el estadístico puede ignora la corrección por población finita y usa a la formula (2).

Haciendo las sustituciones apropiadas se encuentra que el valor n es:

n = [ (1,96x1,96)x(20x20)]/(5x5)  = 61,44

se le recomienda  que se tome una muestra de 61 personas.

Determinar el tamaño de muestra para estimar proporciones

Este método es esencialmente igual al que se describió anteriormente, suponiendo que el muestreo garantice la normalidad aproximada de la distribución P, se llega a la a la siguiente fórmula es decir
                           2     
 cambiar    S  por PxQ

donde P es la proporción en la población que posee la característica de interés, y obviamente es el parámetro que se esta tratando de estimar , veamos un ejemplo

Ejemplo 2

Se está planeando una encuesta con el fin de determinar qué proporción de familias en cierta área son medicamente indigentes. Se tiene la impresión de que la proporción no puede ser mayor que 35%. Se desea un intervalo de confianza del 95% con un error del 5 %. ¿Qué tamaño de muestra de familias debe seleccionarse?



                                                      2           
                                               Z    PxQ 
                                   no = ----------------                       
                                                     2
                                               e 


Sustituimos


                                                      2           
                                            1,96x.(0,35)x(0,65) 
                                   n = --------------------------------------------    = 349,6                   
                                                                   2
                                               (0,05)

Entonces el tamaño de muestra es de 350.

La Aleatoriedad

 
De un modo muy general, podemos decir que la probabilidad es la disciplina que se ocupa del estudio de lo aleatorio (o estocástico) y que un proceso estocástico es el estudio de lo aleatorio cuando se incorpora la variable tiempo. Por ejemplo, lo que sucede al lanzar una moneda no es un proceso estocástico; sin embargo, la secuencia de resultados obtenidos al lanzar una moneda varias veces seguidas sí que lo es.

No importa cuanto se sepa acerca de una acción financeira, aun no se puede saber con certeza como cambiara el precio a continuación, de la misma manera, no importa cuanto sepa sobre una moneda antes que se voltee, aun no puede predecir a que valor llegara después. El factor común: La Aleatoriedad

En el campo de las telecomunicaciones encontramos distintas áreas que requieren del “control ”de lo aleatorio. Nos servimos de la teoría de la señal para ilustrar el concepto de aleatorio en este campo. Una señal aleatoria es una onda en el tiempo que sólo puede caracterizarse mediante la probabilidad. Más concretamente, una señal de radio o televisión, cuya emisión está muy controlada, pues llegar al receptor con ciertas perturbaciones como pitidos de fondo o “nieve”en la imagen. La onda que se superpone a la emisión de la radio o de la televisión es una tensión que vista en el osciloscopio fluctúa aleatoriamente (sin un patrón específico) en el tiempo. Esta onda se denomina ruido. La señal anterior es inherente a cualquier emisión considerada en el campo de la telecomunicación y no es en absoluto deseable, es un “mal”con el que se convive. Ahora bien, también hay señales aleatorias deseables, como puede ser la sucesión de ceros y unos (bits) que transmite un ordenador, la energía eléctrica producida por un aerogenerador, la señal producida por un detector solar, etc. El hecho de que las señales anteriores sean aleatorias se debe a que hay fenómenos aleatorios que las generan, como la fuente de información a la que accede el ordenador, la velocidad del viento o las condiciones meteorológicas.

Según Wikipedia: "La aleatoriedad se asocia a todo proceso cuyo resultado no es previsible más que en razón de la intervención del azar. El resultado de todo suceso aleatorio no puede determinarse en ningún caso antes de que este se produzca. El estudio de los fenómenos aleatorios queda dentro del ámbito de la teoría de la probabilidad y, en un marco más amplio, en el de la estadística.
La palabra aleatorio se usa para expresar una aparente carencia de propósito, causa, u orden. El término aleatoriedad se usa a menudo como sinónimo con un número de propiedades estadísticas medibles, tales como la carencia de tendencias o correlación."


El concepto de aleatoriedad y el papel que desempeña en la naturaleza ha ocupado a los investigadores desde hace siglos. En sus días, pensadores como Leibniz y Laplace desterraron el azar del funcionamiento del mundo al sostener que nada ocurre sin que haya una razón para ello y que todo proceso natural debería poder predecirse sin ambigüedades una vez se conociesen por completo todas las condiciones iniciales de un sistema. En el siglo XX, sin embargo, la mecánica cuántica cambió las reglas del juego y reclamó para sí una noción de aleatoriedad intrínseca en las leyes físicas. Desde entonces, un sinfín de experimentos han demostrado que la naturaleza, después de todo, sí es capaz de llevar a cabo «actos de creación pura».


Un sistema es aleatorio, cuando no se puede predecir un resultado con certeza, incluso cuando se tiene toda la información disponible. Pero puede explorar el comportamiento de sistemas aleatorios utilizando modelos matemáticos, que operan en el mundo de las probabilidades, que describen el comportamiento probable de los sistemas aleatorios bajo diferentes condiciones

Algunos ejemplos complejos:

a) El numero esperado de llamadas telefónicas que llegan por minuto a una centralita es de 10. Simular una realización del proceso que cuenta el numero de llamadas hasta el minuto i, con i = 1, . . . , 100. Consideramos la hipótesis  habitual de que el numero de llamadas por unidad de tiempo se comporta como una Poisson.

b) Un observatorio meteorológico realiza mediciones cada 5 minutos de la temperatura en el exterior en un día caluroso de agosto en el que no hay grandes alteraciones climatologícas.

c) Un parque eólico tiene un potente anemómetro que mide permanentemente la velocidad del viento en metros por segundo. Durante un seguimiento continuo de una hora, observamos velocidades que se comportan como una distribución gamma de parámetros α = 2 y β = 2.

d) El sistema de alarma de un edificio tiene un sensor que transmite la senal 0 mientras no detecta una intensidad de corriente superior a 20 amperios, en el momento que lo detecta transmite un valor igual a uno. Suponemos que la intensidad de corriente, I, se comporta como una exponencial trasladada 15 unidades. Esto es, I = 15 + X, donde X ∼ ξ(0.25).

Para finalizar, vean el esquema de un proceso estocástico

>

Una opinión sobre las encuestas

Las encuestas son interesantes instrumentos de medición y como tales, cada quien le da el uso que desee. Para evaluar su confiabilidad sugiero tomar en cuenta el tamaño de la muestra, la precisión, el error típico, el grado de confiabilidad, la ubicación geográfica, los costos asociados y el mecanismo ha implementar para la medición.

La necesidad de que en  las investigaciones por muestreo (lo que comúnmente se denomina "Encuesta"), hay que definir varios aspectos a la hora de realizarla.

1.- Establecer el diseño muestral, que es la columna vertebral del estudio.

2.-Precisar las Variables a medir incluyendo los costos.

3.- Los objetivos

4.- Definir conceptualmente el fenómeno a estudiar.

Esta es una disciplina científica, pero  hay quien la considera como una bola de cristal, sin embargo los Estadísticos hacemos un seguimiento del comportamiento del mercado e identificamos los posibles escenarios, por ejemplo, en los estudios políticos o electorales,  se plantean varios escenarios para obtener el porcentaje (%)  en intención de votos de los aspirantes a algún cargo público, además se plantean varios escenarios en la manera como se fueran a distribuir los encuestados que no dicen por quien va a votar.

Siempre debe haber un rigor en el análisis y resultados de las encuestas y no deben estar sesgada por algún tipo de interés, ademas se debe de estudiar con mucho cuidado su metodología que nos permita encontrar razones porque nos lleva a un pronostico determinado, para que luego se pueda leer, interpretar y analizar  los resultados correctamente.

La publicación de las encuestas son relevantes para los habitantes de un país, quienes cada día aspiran a tener mas información y mayor interés por los estudios de opinión, mas allá  de que existan buenas y malas encuestadoras y por otro lado si hay una sociedad que piensa que le mienten tanto los servidores públicos como las instituciones. Por tales razones hay forma de interpretar la realidad y por ende se necesita de instrumentos de medición con calidad y que sean comparables.

Se debe tener unos standares mínimos que permitan que una encuesta sea mas o menos confiables para los ciudadanos de las nuevas y venideras sociedades, que puedan revisar los diferentes estudios de opinión con una credibilidad aceptable.

Es importante resaltar, que los estudios de opinión, independientemente de los resultados que arrojen, desatan lo que le llaman "pasiones" porque en los grupos sociales crea un fervor para las  conversas y discusiones al respecto.

Hay varios mitos sobre las encuestas, uno de ellos es que "las encuestas son manipuladas por quienes la pagan". Si fuera cierto, en vez de contratar a una empresa encuestadora, la persona o grupo podría escribir en una hoja unos datos, gráficas y las presenta. Otro mito es "la encuesta es una fotografía del momento", en países como el nuestro donde hay una hiperinflación exagerada, esa condición cambia diariamente y las encuesta que se hace hoy, y mañana se la hacen a la misma persona y esa respuesta es totalmente diferente, ademas que tratan de justificarse por los errores que cometen en las predicciones, proyecciones y análisis e interpretación de resultados, ya que cuando se hace un estudio por muestreo se supone que se va a inferir sobre algún fenómeno de estudio, para un tiempo determinado. Otro mito es " los instrumentos de medición pueden ser visto como buenos y malos", ya que estos son elaborados a petición del cliente y no para ser divulgado en medios de comunicación para resaltar unas pocas características que se quieren que se resalten,las mismas deben de tener un rigor técnico y que sean confiable.

Para culminar, ofrezco un esquema de como puede realizarse una investigación por muestreo:

• Plantear los Objetivos y finalidades
• Terminología y conceptos. Medidas estadísticas a utilizar
• Cuestionarios  ( se diseñan conforme a los objetivos del estudio y el periodo de investigación)
• Universo de estudio
• Diseño, tamaño y selección de las muestras
• Encuesta previa o piloto
• Encuesta definitiva
• Costos asociados a la investigación
• Periodo y tipo de observación
• Levantamiento de las encuestas
• Calculo de errores de muestreo-Inferencia sobre los resultados muestrales
• Tabulación y análisis de resultados

Fredy Zavarce

Estadístico -UCV

Especialista en Finanzas-UCV

Profesor del Post grado UCV

Profesor de UCV-CUFM

Cátedras: Estadística - Matemáticas y

Modelos Cuantitativos

correo: zavafree@gmail.com

Una teoría matemática de la comunicación

Hace 70 años esta semana Claude Shannon introdujo el campo de la teoría de la información con su ponencia "una teoría matemática de la comunicación", que ha sido citado más de 100, 000 veces: http://bit.ly/2H0ZxvR (Via @TheSIAMNew

"70 years ago this week Claude Shannon ushered in the field of information theory with his paper "A Mathematical Theory of Communication", which has been cited over 100,000 times": http://bit.ly/2H0ZxvR  (via @TheSIAMNews)

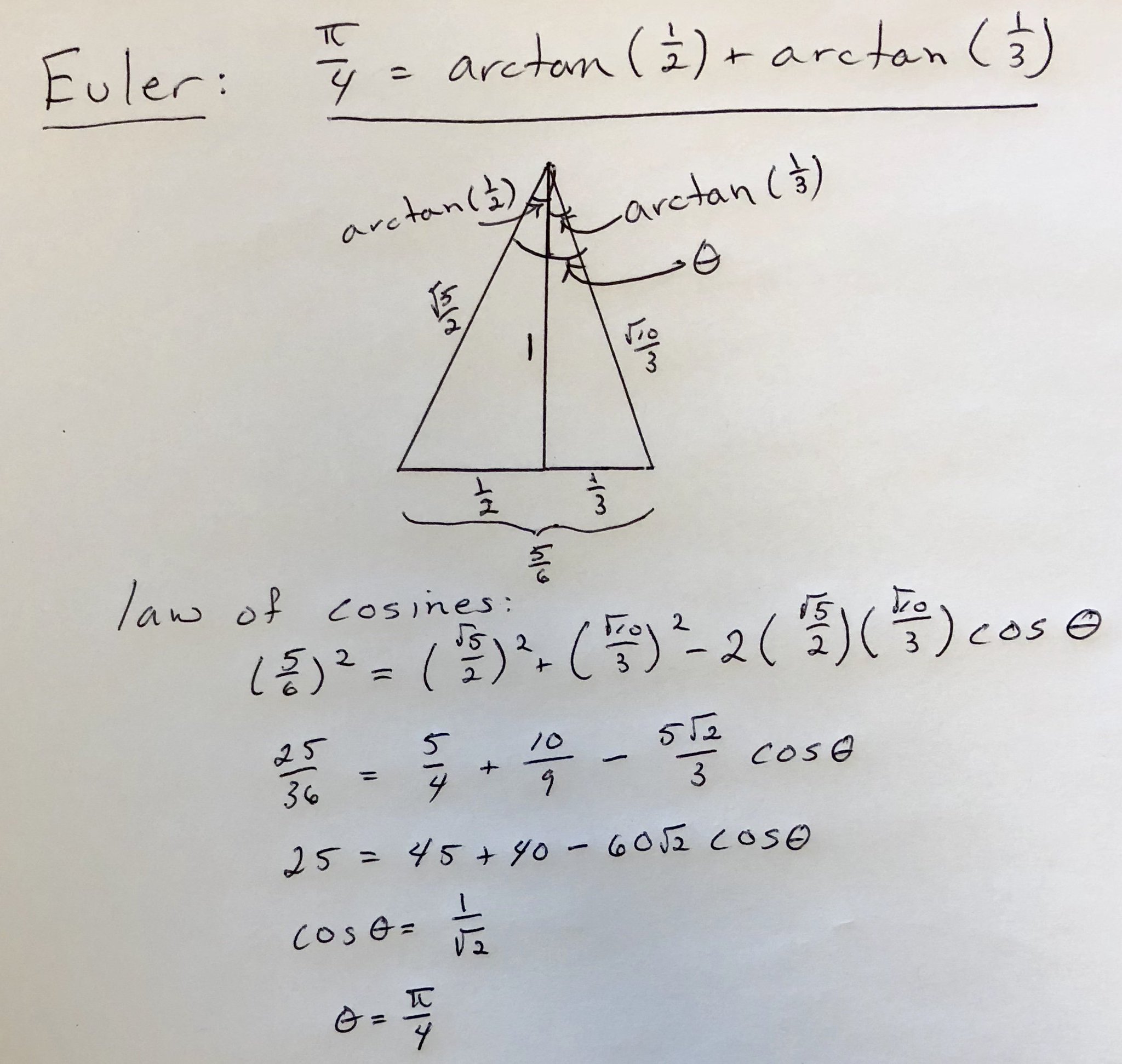
Euler proved that π/4=arctan(1/2)+arctan(1/3), which can be used for computing digits of π (using the arctangent series). I wondered if I could prove it without using a trig identity for tangent (which I'd have to look up). Good news: Easy to do using the law of cosines.

Euler demostró que π / 4 = arctan (1/2) + arctan (1/3), que se puede usar para calcular los dígitos de π (usando la serie arctangent). Me preguntaba si podría probarlo sin usar una identidad trigonométrica para la tangente (que tendría que buscar). Buenas noticias: fácil de hacer usando la ley de los cosenos.